Краткий конспект подготовки к ЗНО по математике №30 "Функции"
Урок 30. Функции
Тригонометрические функции
1. Функция синус
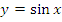 – график функции синусоида.
– график функции синусоида.
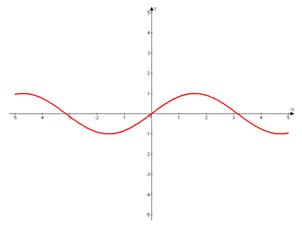
Свойства:
а) Область определения: 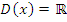 ;
;
б) Область значений: 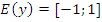 ;
;
в) Функция имеет период 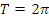 ;
;
г) Функция нечетная: 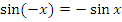 ;
;
д) На интервале 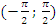 функция монотонно возрастает, на интервале
функция монотонно возрастает, на интервале 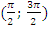 – монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
– монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция непрерывна.
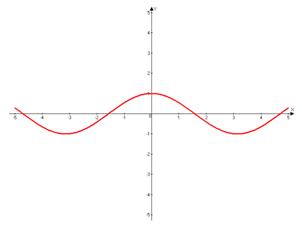
2. Функция косинус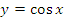 – график функции синусоида, сдвинутая на
– график функции синусоида, сдвинутая на 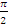 влево относительно оси ординат.
влево относительно оси ординат.
Свойства:
а) Область определения: 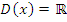 ;
;
б) Область значений: 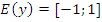 ;
;
в) Функция имеет период 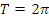 ;
;
г) Функция четная: 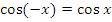 ;
;
д) На интервале 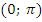 функция монотонно убывает, на интервале (
функция монотонно убывает, на интервале ( – монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
– монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция непрерывна.
3. Функция тангенс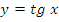
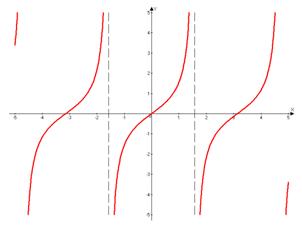
Свойства:
а) Область определения: 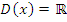 кроме
кроме 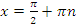 , где
, где 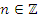 ;
;
б) Область значений: 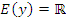 ;
;
в) Функция имеет период 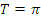 ;
;
г) Функция нечетная: 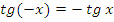 ;
;
д) На интервале 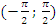 функция монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
функция монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция имеет разрывы и вертикальные асимптоты 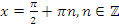 .
.
4. Функция котангенс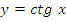
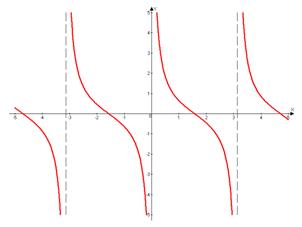
Свойства:
а) Область определения: 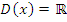 кроме
кроме 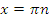 , где
, где 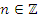 ;
;
б) Область значений: 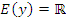 ;
;
в) Функция имеет период 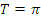 ;
;
г) Функция нечетная: 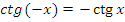 ;
;
д) На интервале 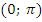 функция монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
функция монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция имеет разрывы и вертикальные асимптоты 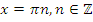 .
.
Обратные тригонометрические функции
1. Функция арксинус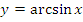
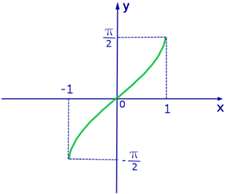
Свойства:
а) Область определения: 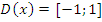 ;
;
б) Область значений: 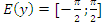 ;
;
в) Функция не периодичная;
г) Функция нечетная: 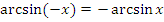 ;
;
д) Функция монотонно возрастает на всей области определения;
е) Функция непрерывна.
2. Функция арккосинус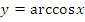
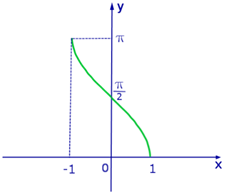
Свойства:
а) Область определения: 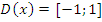 ;
;
б) Область значений: 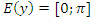 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения;
е) Функция непрерывна.
3. Функция арктангенс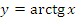
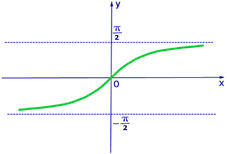
Свойства:
а) Область определения: 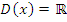 ;
;
б) Область значений: 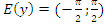 ;
;
в) Функция не периодичная;
г) Функция нечетная: 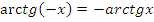 ;
;
д) Функция монотонно возрастает на всей области определения;
е) Функция непрерывна.
4. Функция арккотангенс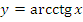
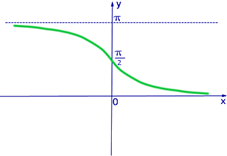
Свойства:
а) Область определения: 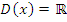 ;
;
б) Область значений: 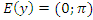 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения;
е) Функция непрерывна.
Показательная функция
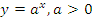
В данном случае необходимо рассматривать два случая.
1. Основание степени больше единицы: 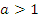 .
.
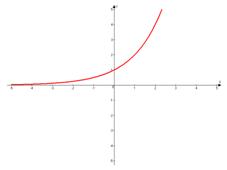
Свойства:
а) Область определения: 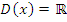 ;
;
б) Область значений: 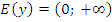 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно возрастает на всей области определения и имеет горизонтальную асимптоту 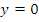 ;
;
е) Функция непрерывна.
2. Основание степени меньше единицы: 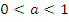 .
.
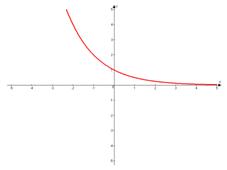
Свойства:
а) Область определения: 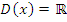 ;
;
б) Область значений: 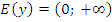 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения и имеет горизонтальную асимптоту 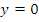 ;
;
е) Функция непрерывна.
Логарифмическая функция
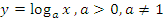
Здесь также необходимо рассматривать два случая.
1. Основание логарифма больше единицы: 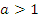 .
.
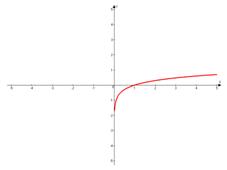
Свойства:
а) Область определения: 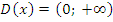 ;
;
б) Область значений: 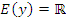 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно возрастает на всей области определения и имеет вертикальную асимптоту 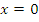 ;
;
е) Функция непрерывна.
2. Основание логарифма меньше единицы: 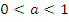 .
.
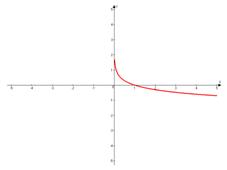
Свойства:
а) Область определения: 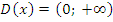 ;
;
б) Область значений: 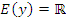 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения и имеет вертикальную асимптоту 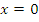 ;
;
е) Функция непрерывна.
Преобразование графиков функций
Выше были представлены графики некоторых простейших функций. Также ранее мы уже изучали графики линейной, квадратичной и др. функций (см. конспект №10). Графики большинства более сложных функций можно получить, преобразовывая известные графики простейших функций.
Рассмотрим ряд правил преобразования графиков функций.
| Преобразование | Пример |
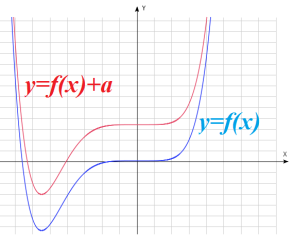
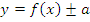 : график получается путем сдвига графика функции : график получается путем сдвига графика функции 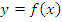 на a единиц вверх (при «+») или вниз (при «-») на a единиц вверх (при «+») или вниз (при «-») |
|
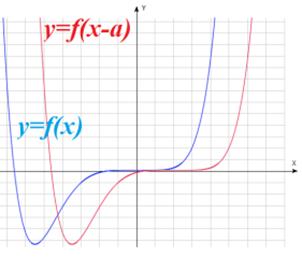
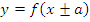 : график получается путем сдвига графика функции : график получается путем сдвига графика функции 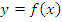 на a единиц влево (при «+») или вправо (при «-») на a единиц влево (при «+») или вправо (при «-») |
|
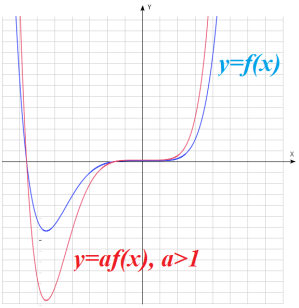
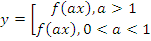 : график получается путем сжатия ( : график получается путем сжатия (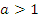 ) или растяжения ( ) или растяжения (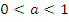 ) графика функции ) графика функции 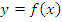 в a раз относительно оси ординат в a раз относительно оси ординат |
|
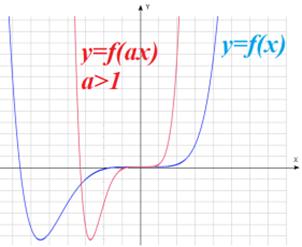
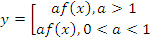 : график получается путем растяжения ( : график получается путем растяжения (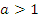 ) или сжатия ( ) или сжатия (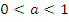 ) графика функции ) графика функции 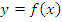 в a раз относительно оси абсцисс в a раз относительно оси абсцисс |
|
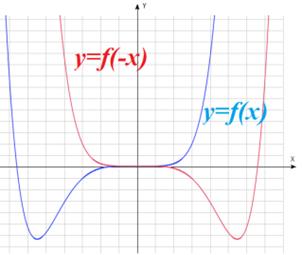
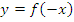 : график получается путем симметричного отображения графика функции : график получается путем симметричного отображения графика функции 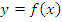 относительно оси ординат относительно оси ординат |
|
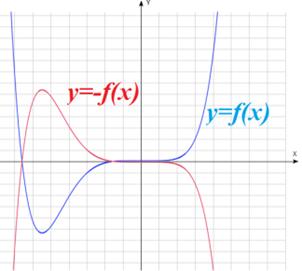
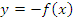 : график получается путем симметричного отображения графика функции : график получается путем симметричного отображения графика функции 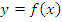 относительно оси абсцисс относительно оси абсцисс |
|
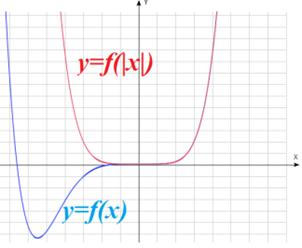
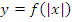 : график получается путем добавления симметричного отображения части графика функции : график получается путем добавления симметричного отображения части графика функции 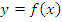 , которая построена при , которая построена при 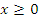 , относительно оси ординат и отбрасывания части графика функции, которая построена при , относительно оси ординат и отбрасывания части графика функции, которая построена при 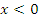 |
|
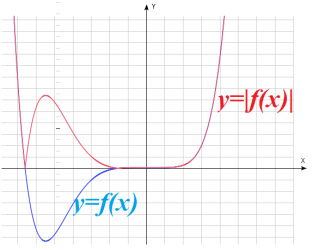
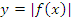 : график получается путем симметричного отображения отрицательной части графика функции : график получается путем симметричного отображения отрицательной части графика функции 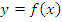 относительно оси абсцисс, при этом положительная часть графика остается без изменений относительно оси абсцисс, при этом положительная часть графика остается без изменений |
|
Краткий конспект подготовки к ЗНО по математике №29 Функции
Урок 29. Функции
Понятие функциональной зависимости
Функциональная зависимость устанавливает правило, согласно которому по значению независимой переменной – аргумента, можно найти значение зависимой переменной – функции. Слово функция употребляют в двух значениях: это и сама функциональная зависимость, и зависимая переменная.
Самое главное требование к функциональной зависимости: единственность от аргумента к функции. Это означает, что каждому значению аргумента может соответствовать единственное значение функции, в то время как одному значению функции может соответствовать сколь угодно много значений аргумента.
Функция - это закон соответствия между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует только одно определенное значение другой величины y (функции или зависимой переменной).
Основные способы задания числовых функций:
1. Аналитический способ – задание функции с помощью формулы.
Обозначать в общем виде такую формулу принято обычно как 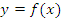 , где под x понимают аргумент, а под y значение функции.
, где под x понимают аргумент, а под y значение функции.
2. Табличный способ – задание функции с помощью таблицы связанных друг с другом значений.
3. Графический способ – задание функции с помощью изображения точек в системе координат, когда одной координате точек поставлена в однозначное соответствие другая ее координата.
Область определения и область значений
Область определения функции – это множество значений аргумента, для которых функция имеет смысл. Иными словами, это допустимые значения икса. Это множество принято обозначать D или D(x).
Если функция задана аналитически, как это чаще всего бывает, то в таком случае удобнее всего сначала найти те значения аргумента, при которых функция не имеет смысла, и исключить их из множества действительных чисел.
Основные случаи, в которых необходимо искать не имеющие смысла для функции аргументы:
1. Наличие в функции деления на выражение, содержащее неизвестную. В таком случае исключаются те аргументы, при которых возникает деление на ноль.
2. Присутствие в функции корня четной степени из выражения, содержащего неизвестную. При этом необходимо исключить аргументы, при которых подкоренное выражение отрицательно, в таком случае удобно сразу накладывать условие, что подкоренное выражение больше или равно нулю.
3. Наличие в функции логарифмов, содержащих неизвестные выражения. В общем виде это можно записать так: если функция содержит 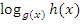 , где g(x) и h(x) - это выражения, содержащие неизвестную, то областью определения будет решение системы неравенств
, где g(x) и h(x) - это выражения, содержащие неизвестную, то областью определения будет решение системы неравенств 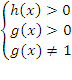 .
.
Область значений функции – это множество значений функции, которые она принимает в своей области определения. Т.е. в стандартной записи функции это значения ее игрека. Множество значений функции принято обозначать E или E(y).
Задания на поиск области значений функции в ВНО встречаются достаточно редко.
Понятия четности и монотонности
Функция называется четной, если для всех значений аргумента верно следующее –при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так 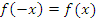 .
.
График такой функции симметричен относительно оси 0y.
Пример: 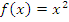 .
. 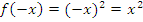 – функция четная.
– функция четная.
Функция называется нечетной, если для всех значений аргумента верно следующее – при изменении знака аргумента, она меняет свое значение на противоположное. Формульная запись этого выглядит так 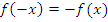 .
.
График такой функции симметричен относительно начала координат.
Пример: 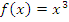 .
. 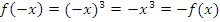 – функция нечетная.
– функция нечетная.
Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида. У таких функций нет симметрии относительно оси 0y и начала координат.
Важным свойством функции является ее монотонность. Выделяют следующие виды монотонности функций:
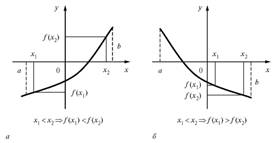
1. Функция f(x) возрастает, если на некотором интервале, если для любых двух точек 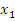 и
и 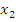 этого интервала таких, что
этого интервала таких, что 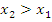 выполнено, что
выполнено, что 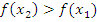 . Т.е. большему значению аргумента соответствует большее значение функции;
. Т.е. большему значению аргумента соответствует большее значение функции;
2. Функция f(x) убывает, если на некотором интервале, если для любых двух точек 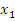 и
и 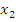 этого интервала таких, что
этого интервала таких, что 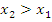 выполнено, что
выполнено, что 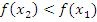 . Т.е. большему значению аргумента соответствует меньшее значение функции;
. Т.е. большему значению аргумента соответствует меньшее значение функции;
3. Функция f(x) неубывает, если на некотором интервале, если для любых двух точек 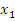 и
и 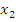 этого интервала таких, что
этого интервала таких, что 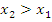 выполнено, что
выполнено, что 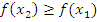 ;
;
4. Функция f(x) невозрастает, если на некотором интервале, если для любых двух точек 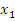 и
и 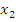 этого интервала таких, что
этого интервала таких, что 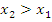 выполнено, что
выполнено, что 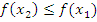 .
.
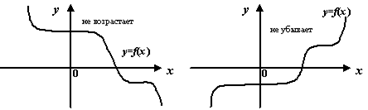
Для первых двух случаев еще применяют термин «строгая монотонность».
Два последних случая являются специфическими и задаются обычно в виде композиции из нескольких функций.
Пример: Функция 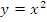 монотонно убывает при
монотонно убывает при 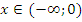 и монотонно возрастает при
и монотонно возрастает при 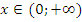 .
.
Обратные функции
Если функция 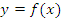 достигает каждого своего значения в единственной точке ее области определения, то можно задать функцию
достигает каждого своего значения в единственной точке ее области определения, то можно задать функцию 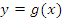 , которая называется обратной к функции
, которая называется обратной к функции 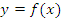 . Причем, для каждого a из области определения f, если
. Причем, для каждого a из области определения f, если 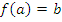 , то
, то 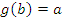 . Функции f и g называются взаимнообратными.
. Функции f и g называются взаимнообратными.
График обратной функции симметричен графику прямой функции относительно прямой 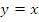 .
.
Периодические функции
Функция 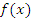 называется периодической с периодом
называется периодической с периодом 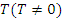 , если для любого x верно: если функция определена в одной из точек x или
, если для любого x верно: если функция определена в одной из точек x или 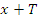 , то она определена и во второй точке, а значения функции в обеих точках равны, то есть
, то она определена и во второй точке, а значения функции в обеих точках равны, то есть 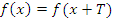 .
.
Число T называется периодом функции.
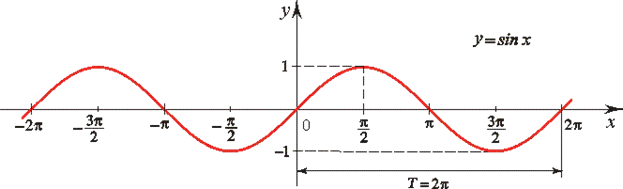
Все тригонометрические функции являются периодическими.
Понятие ГМТ
Графическое изображение однозначной функции называют построением графика функции, а изображение многозначной функции – построением геометрического места точек или ГМТ.
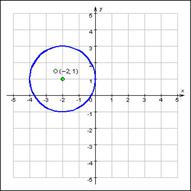
Пример: Графическое изображение уравнения 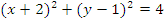 будет ГМТ, а конкретно изображением окружности:
будет ГМТ, а конкретно изображением окружности:
Краткий конспект подготовки к ЗНО по математике №21-22 "Логарифмы. Логарифмические уравнения и неравенства"
Конспект 21-22. Логарифмы. Логарифмические уравнения и неравенства
Определение логарифма, основное логарифмическое тождество
Логарифмом числа b по основанию a (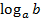 ) называют показатель степени, в которую нужно возвести число a, чтобы получить число b:
) называют показатель степени, в которую нужно возвести число a, чтобы получить число b: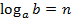 , если
, если 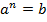 , ОДЗ: a,b>0, a≠1.
, ОДЗ: a,b>0, a≠1.
Для удобства приняты сокращенные обозначения логарифмов, которые часто встречаются в разных областях науки:
1) Натуральным логарифмом (ln a) называют логарифм по основанию e≈2,7 – число Непера.
2) Десятичным логарифмом (lg a) называют логарифм по основанию 10.
Основное логарифмическое тождество: 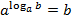 .
.
Это тождество следует из определения логарифма: так как логарифм – это показатель степени (n), то, возводя в эту степень число a, получим число b.
Свойства логарифмов
При условии, что a,b,c>0,a≠1:
1)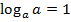 ;
;
2) 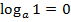 ;
;
3) 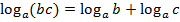 – логарифм произведения равен сумме логарифмов;
– логарифм произведения равен сумме логарифмов;
4) 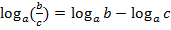 – логарифм частного равен разности логарифмов;
– логарифм частного равен разности логарифмов;
5) 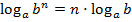 ;
;
6) 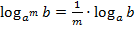 ;
;
7) 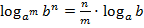 ;
;
8) 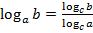 , c≠1 – переход к новому основанию логарифма;
, c≠1 – переход к новому основанию логарифма;
9) 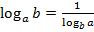 , b≠1.
, b≠1.
Преобразование выражений, содержащих логарифмы
Пример: Вычислить 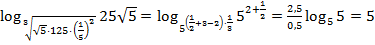 .
.
Пример: Вычислить 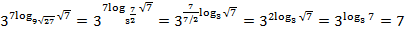 .
.
Пример: Вычислить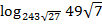 , если
, если 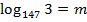 .
.
Решение: 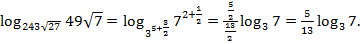 .
.
Теперь рассмотрим то, что дано по условию:
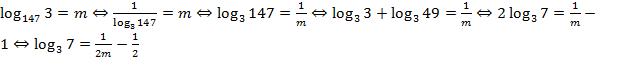 .
.
Подставим это в исходное преобразованное выражение: 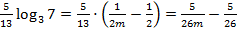 .
.
Ответ: 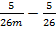 .
.
Основные методы решения логарифмических уравнений и неравенств
Простейшее логарифмическое уравнение имеет вид:
1) 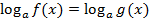 , что соответствует простейшему уравнению f(x)=g(x) с учетом ОДЗ логарифмической функции;
, что соответствует простейшему уравнению f(x)=g(x) с учетом ОДЗ логарифмической функции;
2) 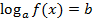 , что решается по определению логарифма.
, что решается по определению логарифма.
Логарифмическое уравнение любой сложности нужно преобразовать до простейшего.
При решении уравнений можно проверять полученные корни по ОДЗ либо выполнять подстановку.
1) Простейшие уравнения вида 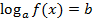 решаются по определению.
решаются по определению.
Пример: Решить 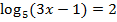 .
.
Решение: 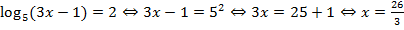 . Выполним подстановку
. Выполним подстановку 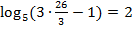 – верное тождество.
– верное тождество.
Ответ: 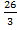 .
.
2) Уравнения вида 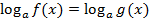 .
.
Пример: Решить 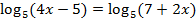 .
.
Решение: 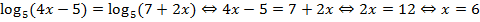 . Подстановка
. Подстановка 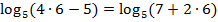 – верное тождество.
– верное тождество.
Ответ: 6.
3) Уравнения вида 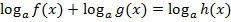 преобразовываются согласно свойствам 3 и 4.
преобразовываются согласно свойствам 3 и 4.
Пример: Решить 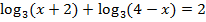 .
.
Решение:
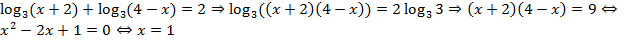 .
.
Подстановка 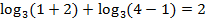 – верное тождество.
– верное тождество.
Ответ: 1.
4) Метод замены переменных. Логарифмические уравнения могут сводиться, например, к квадратным путем замены переменных
Пример: Решить 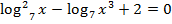 .
.
Решение: 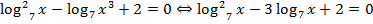 . Удобно ввести замену:
. Удобно ввести замену: 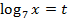 , тогда:
, тогда: 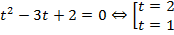 . В исходных переменных:
. В исходных переменных: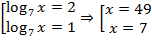 . Подстановка
. Подстановка 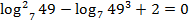 – верное тождество,
– верное тождество, 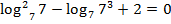 – верное тождество.
– верное тождество.
Ответ: 7;49.
Простейшее логарифмическое неравенство имеет вид:
1) 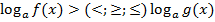 . Здесь нужно рассматривать два случая – аналогично показательным неравенствам. Если основание логарифма больше единицы – логарифмическому неравенству ставится в соответствие простейшее неравенство вида f(x)>(<;≥;≤)g(x), причем знак исходного неравенства сохраняется. Если основание логарифма меньше единицы, то получаем неравенство f(x)<(>;≤;≥)g(x), т.е. знак исходного неравенства меняется на противоположный.
. Здесь нужно рассматривать два случая – аналогично показательным неравенствам. Если основание логарифма больше единицы – логарифмическому неравенству ставится в соответствие простейшее неравенство вида f(x)>(<;≥;≤)g(x), причем знак исходного неравенства сохраняется. Если основание логарифма меньше единицы, то получаем неравенство f(x)<(>;≤;≥)g(x), т.е. знак исходного неравенства меняется на противоположный.
Частью решения неравенства является запись ОДЗ логарифмов, которые в него входят.
2) loga f(x)>(<;≥;≤) b. Оно решается по определению логарифма с проверкой знака неравенства по аналогии с предыдущим пунктом.
Как и в предыдущем случае частью решения неравенства является запись ОДЗ логарифмов.
Логарифмическое неравенство любой сложности нужно преобразовать до простейшего. Основные типы и методы преобразования логарифмических неравенств аналогичны логарифмическим уравнениям.
Пример: Решить неравенство 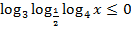 .
.
Решение: Выпишем ОДЗ логарифмов 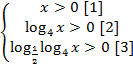 .
.
Перейдем к решению
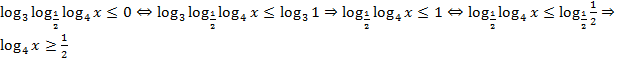
(автоматически выполнено ОДЗ [2]) 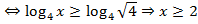 (автоматически выполнено ОДЗ [1]).
(автоматически выполнено ОДЗ [1]).
Осталось решить неравенство из ОДЗ [3] и проверить влияет ли оно на решение. 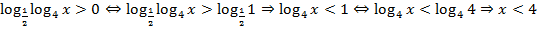 .
.
Объединяем решение ОДЗ с первичным решением неравенства 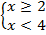 . Как видим, ОДЗ повлияло на итоговое решение.
. Как видим, ОДЗ повлияло на итоговое решение.
Ответ: x∈ [2;4).
Краткий конспект подготовки к ЗНО по математике №19-20 "Показательные уравнения и неравенства"
Урок 19-20. Показательные уравнения и неравенства
Преобразование выражений со степенями (повторение, закрепление)
Пример: Упростить выражение 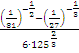
Решение: 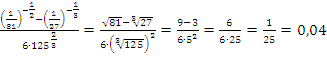
Ответ: 0,04.
Методы решения показательных уравнений и неравенств
Простейшее показательное уравнение имеет вид: 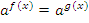 , где a – действительное число, a>0.
, где a – действительное число, a>0.
В таком случае показательное уравнение заменяется более простым, чаще всего линейным или квадратным, вида: 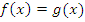 . При решении показательных уравнений любой сложности цель – привести уравнение к виду
. При решении показательных уравнений любой сложности цель – привести уравнение к виду 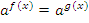 и перейти к уравнению
и перейти к уравнению 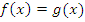 .
.
Пример: Решить уравнение 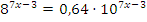 .
.
Решение: Обе части уравнения нужно поделить на 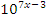 :
: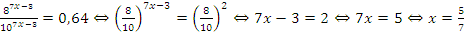 .
.
Ответ:  .
.
Некоторые показательные уравнения сводятся к квадратным.
Пример: Решить уравнение 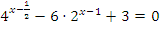
Решение: 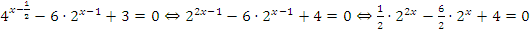 .
.
Удобно выполнить замену переменных 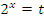 :
: 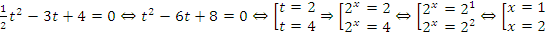 .
.
Ответ: 1; 2.
Уравнения вида 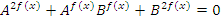 называются однородными и решаются путем деления всего уравнения на одну из старших степеней
называются однородными и решаются путем деления всего уравнения на одну из старших степеней 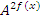 или
или 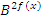 . Далее вводится замена вида
. Далее вводится замена вида ![]()
Пример: Решить уравнение 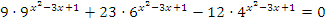 .
.
Решение: Нужно выполнить деление: 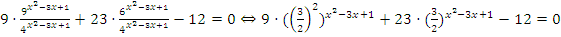 . Теперь нужно ввести замену переменных:
. Теперь нужно ввести замену переменных: 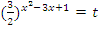 , тогда:
, тогда: 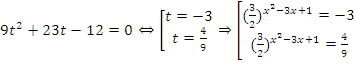 .
.
Первое уравнение не имеет смысла, т.к. показательная функция не принимает отрицательных значений. Второе уравнение – простейшее показательное уравнение, от которого следует перейти к квадратному.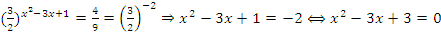 . У данного уравнения нет корней, т.к. его дискриминант отрицательный. Следовательно нет корней и у исходного уравнения.
. У данного уравнения нет корней, т.к. его дискриминант отрицательный. Следовательно нет корней и у исходного уравнения.
Ответ: корней нет.
Простейшее показательное неравенство имеет вид: 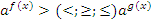 , где a – действительное число, a>0.
, где a – действительное число, a>0.
Здесь нужно рассматривать два случая:
– когда основание степени a больше единицы, показательное неравенство заменяется более простым, чаще всего линейным или квадратным, вида: 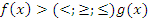 , при чем сохраняется знак исходного неравенства;
, при чем сохраняется знак исходного неравенства;
– если же основание степени меньше единицы, то знак исходного неравенства следует поменять на противоположный.
При решении показательных неравенств любой сложности цель – привести неравенство к простейшему.
Основные типы показательных неравенств и методы их преобразования аналогичны показательным уравнениям.
Пример: Решить неравенство 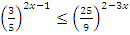 .
.
Решение: Приводим к одинаковому основанию 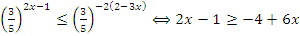 , знак неравенства поменяли, т.к.
, знак неравенства поменяли, т.к. 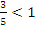 . Далее решаем линейное неравенство и получаем
. Далее решаем линейное неравенство и получаем 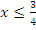 .
.
Ответ: 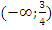 .
.
Системы показательных уравнений
Пример: Решить систему 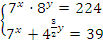 .
.
Решение: 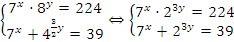 . Нужно ввести замену переменных:
. Нужно ввести замену переменных: 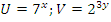 , тогда:
, тогда: 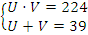 . Такая система удобно решается методом подстановки, ее решение:
. Такая система удобно решается методом подстановки, ее решение: 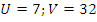 и
и 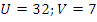 . В исходных переменных:
. В исходных переменных: 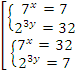 – получена совокупность систем простейших показательных уравнений. Метод решения уравнений, которые входят в первую систему, нам уже известен, для решения второй нам понадобятся знания логарифмов, которые мы изучим в следующих темах.
– получена совокупность систем простейших показательных уравнений. Метод решения уравнений, которые входят в первую систему, нам уже известен, для решения второй нам понадобятся знания логарифмов, которые мы изучим в следующих темах.
Пример: 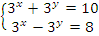 .
.
Решение: Здесь нужно применить такой прием: получить новую систему, первое уравнение которой это сумма исходных уравнений, а второе – разность. 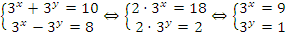 – получена система простейших показательных уравнений, метод решения которых нам уже известен.
– получена система простейших показательных уравнений, метод решения которых нам уже известен.
Краткий конспект подготовки к ЗНО по математике №17-18 "Иррациональные уравнения и неравенства"
Урок 17-18. Иррациональные уравнения и неравенства
Решение иррациональных уравнений
Иррациональными называются такие уравнения, в которых переменная стоит под знаком корня.
1) Уравнения вида 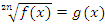 или
или 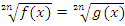 решаются путем возведения обеих частей в степень корня. Здесь обязательна проверка полученных корней, так как под корнем четной степени может стоять только положительное число или ноль и сам корень может принимать только неотрицательные значения.
решаются путем возведения обеих частей в степень корня. Здесь обязательна проверка полученных корней, так как под корнем четной степени может стоять только положительное число или ноль и сам корень может принимать только неотрицательные значения.
2) Уравнения вида 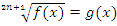 или
или 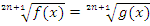 решаются путем возведения обеих частей в степень корня. Здесь проверка не нужна, так как под корнем может стоять любое действительное число и сам корень принимает любые значения.
решаются путем возведения обеих частей в степень корня. Здесь проверка не нужна, так как под корнем может стоять любое действительное число и сам корень принимает любые значения.
Пример: Решить уравнение 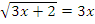 .
.
Решение: 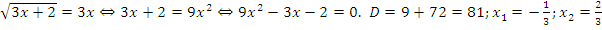
Проверка: 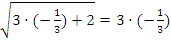 . Квадратный корень принимает отрицательное значение, что невозможно – данный корень лишний.
. Квадратный корень принимает отрицательное значение, что невозможно – данный корень лишний. 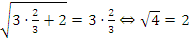 , т.е. корень
, т.е. корень 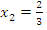 подходит.
подходит.
Ответ: 2/3.
Решение иррациональных неравенств
Иррациональными называются такие неравенства, в которых переменная стоит под знаком корня.
1) Неравенство вида 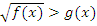 . При решении необходимо рассмотреть два случая:
. При решении необходимо рассмотреть два случая:
а) если правая сторона неравенства неотрицательна, то мы имеем выражение вида «неотрицательное число»>«неотрицательное число», что выполнено не всегда и его необходимо полноценно решать
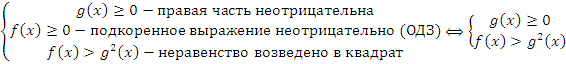
Стоит обратить внимание, что второе условие выполнено автоматически, если выполнено третье, т.е. его можно не записывать при решении.
б) или если правая сторона неравенства отрицательна, то имеем выражение вида «неотрицательное число»>«отрицательное число», что выполнено всегда с учетом ОДЗ, т.е.
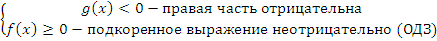
Множества из решений обоих случаев объединяют и получают ответ.
Пример: Решить неравенство 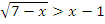 .
.
Решение:
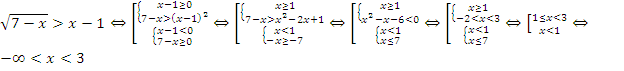
Ответ: 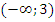
2) Неравенство вида 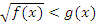 . При решении достаточно рассмотреть одну эквивалентную систему неравенств:
. При решении достаточно рассмотреть одну эквивалентную систему неравенств: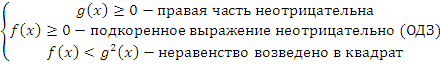
В отличие от предыдущего варианта случай 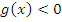 не имеет смысла, так как тогда мы получаем выражение вида «неотрицательное выражение»<«отрицательное выражение», что невозможно.
не имеет смысла, так как тогда мы получаем выражение вида «неотрицательное выражение»<«отрицательное выражение», что невозможно.
3) Неравенства вида 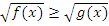 заменяются эквивалентной системой:
заменяются эквивалентной системой: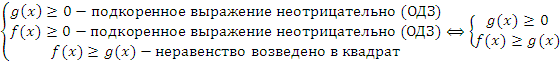
Второе условие выполнено автоматически при выполнении третьего, поэтому его можно не писать.
4) Неравенства вида 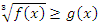 заменяются эквивалентным неравенством:
заменяются эквивалентным неравенством: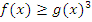 .
.
В них не записываются ограничения на ОДЗ, т.к. подкоренное выражение в корне нечетной степени и сам корень может принимать любые значения.
Замечание. Иррациональные неравенства можно решать графическим методом.
Пример: Решить неравенство графически: 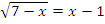 .
.
Решение: Первая функция монотонно убывает, вторая монотонно возрастает на области определения.
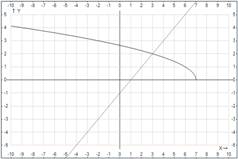
Если уравнение 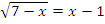 имеет корень, то он единственный, по графику легко его увидеть:
имеет корень, то он единственный, по графику легко его увидеть: 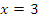 . Эта точка отвечает пересечению, т.е. равенству двух функций.
. Эта точка отвечает пересечению, т.е. равенству двух функций.
Далее по графику выписываем множество аргументов, при которых выполнено неравенство.
Конечно же, такой способ решения эффективен в том случае, когда точки пересечения функций являются целыми и небольшими числами.
Ответ: 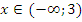 .
.
Неравенства других четных и нечетных степеней решаются аналогично.
Краткий конспект подготовки к ЗНО по математике №14-15 Линейные неравенства. Квадратичные неравенства. Метод интервалов при решении неравенств
Урок 14-15. Линейные неравенства. Квадратичные неравенства. Метод интервалов при решении неравенств
Линейные неравенства
Символическая запись, в которой два числа или выражения, содержащие переменные, связаны знаком «больше» (>) или «меньше» (<), называется неравенством. Наряду со строгими неравенствами (а>b) рассматривают и нестрогие неравенства: а≥b.
Свойства неравенств:
1. Если a>b и b>с, то a>с.
2. Если a>b, то a+с>b+с, с – любое число.
3. Если a>b и с>d, то a+с>b+d. Неравенства одинакового смысла можно почленно складывать.
4. Если a,b,с,d — положительные числа и a>b,с>d, то aс >bd. Неравенства одинакового смысла можно почленно умножать (с учетом знаков).
5. Если a>b ,с<d, то a-с>b-d. Неравенства противоположного смысла можно почленно вычитать, оставляя знак первого неравенства.
Решить неравенство с одной переменной – значит найти все его решения, то есть значения переменной, при которых неравенство истинно, или доказать, что их нет.
Правила решения неравенств:
1) Любое слагаемое неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.
2) Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
3) Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Пример:  ⇔
⇔ ⇔
⇔ ⇔
⇔
Системы и совокупности линейных неравенств
Если неравенства объединены в систему, то решением системы будут те значения переменных, которые удовлетворяют одновременно всем неравенствам. Решение системы соответствует пересечению решений всех неравенств.
Если неравенства объединены в совокупность, то решением ее будут те значения переменных, которые удовлетворяют хотя бы одному из неравенств совокупности. Решение совокупности соответствует объединению решений всех неравенств.
Квадратичные неравенства
Неравенства вида  >(<;≥;≤)0 называются квадратичными. Здесь a,b,c – любые действительные числа, a≠0. Есть несколько случаев решения квадратичных неравенств:
>(<;≥;≤)0 называются квадратичными. Здесь a,b,c – любые действительные числа, a≠0. Есть несколько случаев решения квадратичных неравенств:
1)  ветви параболы направлены вверх, квадратное уравнение имеет два корня. Внутри интервала корней значения квадратного трехчлена отрицательны, вне интервала корней – положительны, в корнях квадратный трехчлен обращается в ноль;
ветви параболы направлены вверх, квадратное уравнение имеет два корня. Внутри интервала корней значения квадратного трехчлена отрицательны, вне интервала корней – положительны, в корнях квадратный трехчлен обращается в ноль;
2)  ветви параболы направлены вверх, квадратное уравнение имеет один корень. Значения квадратного трехчлена положительны при всех значениях аргумента, кроме корня – здесь квадратный трехчлен обращается в ноль;
ветви параболы направлены вверх, квадратное уравнение имеет один корень. Значения квадратного трехчлена положительны при всех значениях аргумента, кроме корня – здесь квадратный трехчлен обращается в ноль;
3)  ветви параболы направлены вверх, квадратное уравнение не имеет корней. Значения квадратного трехчлена положительны при всех значениях аргумента;
ветви параболы направлены вверх, квадратное уравнение не имеет корней. Значения квадратного трехчлена положительны при всех значениях аргумента;
4)  ветви параболы направлены вниз, квадратное уравнение имеет два корня. Внутри интервала корней значения квадратного трехчлена положительны, вне интервала корней – отрицательны, в корнях квадратный трехчлен обращается в ноль;
ветви параболы направлены вниз, квадратное уравнение имеет два корня. Внутри интервала корней значения квадратного трехчлена положительны, вне интервала корней – отрицательны, в корнях квадратный трехчлен обращается в ноль;
5) ветви параболы направлены вниз, квадратное уравнение имеет один корень. Значения квадратного трехчлена отрицательны при всех значениях аргумента, кроме корня – здесь квадратный трехчлен обращается в ноль;
ветви параболы направлены вниз, квадратное уравнение имеет один корень. Значения квадратного трехчлена отрицательны при всех значениях аргумента, кроме корня – здесь квадратный трехчлен обращается в ноль;
6)  ветви параболы направлены вниз, квадратное уравнение не имеет корней. Значения квадратного трехчлена отрицательны при всех значениях аргумента.
ветви параболы направлены вниз, квадратное уравнение не имеет корней. Значения квадратного трехчлена отрицательны при всех значениях аргумента.
Решение рациональных неравенств методом интервалов
Пример:  ≥0
≥0
Решение: При решении примера будет сформулирован общий алгоритм решения неравенств методом интервалов. Он относится и к неравенствам с многочленами и к рациональным неравенствам. Чтобы пользоваться указанным алгоритмом, неравенство изначально следует привести к виду, когда по одну сторону некое выражение, а по другую ноль.
1. Найти нули функции: 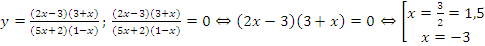
2. Определить ОДЗ: 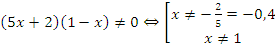
3. Разбить область значений аргумента на интервалы нулями функции и точками разрыва ОДЗ. Точки, которые будут входить в решение неравенства обозначаются закрашенными, а которые не будут входить – выколотыми.
Точки расставляют по следующему принципу:
– закрашенные точки ставятся для нулей функции, если неравенство нестрогое;
– выколотые точки ставятся для нулей функции, если неравенство было строгое, и для точек разрыва ОДЗ функции.
В нашем случае мы поставим на оси координат выколотые точки для x=-0,4 и x=1, а закрашенные для x=1,5 и x=-3.
4. Определить знак функции на каждом интервале.
Для определения знаков есть два способа:
– брать на каждом интервале пробную точку, подставлять ее в функцию и определять знак – такой знак функция будет сохранять на всем интервале;
– с помощью пробной точки определить знак на крайнем правом интервале, а далее чередовать знаки при переходе через точки нулей функции и разрывов ОДЗ. Такой подход верен только при отсутствии множителей в четных степенях и модулей в неравенстве. Следует знать, что если какой-то множитель имеет четную степень, например, функция содержит множитель  , то при переходе через точку x=2 знак функции сохраняется.
, то при переходе через точку x=2 знак функции сохраняется.
Для обозначения знаков промежутков удобно изображать характерную «змейку», которая рисуется над осью координат для положительных значений и под осью для отрицательных значений функции.
В нашем случае проверим, к примеру, знак функции в точке 10 для простоты расчетов:  – функция на крайнем правом интервале отрицательна.
– функция на крайнем правом интервале отрицательна.
Далее на каждом из интервалов просто чередуем знаки функции, т.к. нет множителей в четных степенях и модулей.

5. Выписать в ответ объединение промежутков, которые соответствуют знаку неравенства, т.е. если в неравенстве интересуют значения больше нуля, то выписать промежутки с положительными значениями, и аналогично для других вариантов. Здесь важно помнить о том, что выколотые точки не входят в решение неравенства, а закрашенные точки входят.
Ответ: x∈[-3; -0,4)∪(1;1,5].
Неравенства с модулем
При решении модульных неравенств необходимо учитывать условия раскрывания модулей, а в остальном они решаются как обычные неравенства.
Пример: решить неравенство: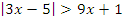 .
.
Решение: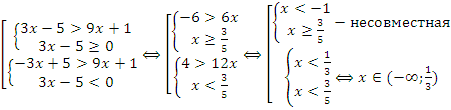
Ответ: x∈(-∞;1/3).
Краткий конспект подготовки к ЗНО по математике №12-13 Решение текстовых задач
Урок 12-13. Решение текстовых задач
Решение любой текстовой задачи состоит из трех этапов:
1) Анализ условия и обозначения величин.
2) Составление модели (уравнений).
3) Решение полученного уравнения (системы уравнений) и получение ответа на вопрос (вопросы) в условии.
Решение задач на пропорции
Решение таких задач основано на понятии пропорции и ее свойствах, которые рассмотрены ранее.
Пример: известно, что с одного гектара фермер собирает 3,5 тонны зерна. Какова площадь поля, если фермер собрал 27 тонн зерна?
Решение: нужно обозначить искомую величину за x и составить пропорцию: 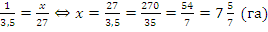 .
.
Ответ: 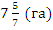 .
.
Решение задач на проценты
Выделяют три типа задач на проценты:
1) Найти, чему равен процент от числа.
2) Пусть задано число A и нужно найти x% от него. Решение: 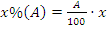 .
.
3) Найти, какой процент от числа составляет данное число.
Пусть заданы числа A и B, требуется определить, сколько процентов число B составляет от числа A. Решение: нужно обозначить искомый процент за x и составить пропорцию 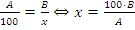 .
.
Найти число, зная, чему равен его процент.
Пусть задано число a, которое составляет x% от некоторого числа A, которое требуется найти. Решение: 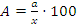 .
.
Пример: Первоначальная стоимость единицы продукции равнялась 75 грн. В течение первого года производства она повысилась на некоторое число процентов, а в течение второго года снизилась (по отношению к повышенной стоимости) на такое же число процентов, в результате чего она стала равна 72 грн. Определите проценты повышения и понижения стоимости единицы продукции.
Решение: нужно обозначить искомый процент за x, тогда в результате повышения цена составит: 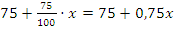 . После понижения:
. После понижения: 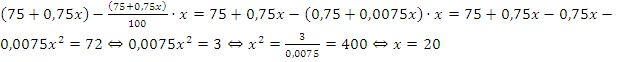 .
.
Ответ: цена изменялась на 20%.
Решение задач на смеси, растворы и сплавы
Решение основывается на формуле: 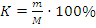 , где K – процент вещества в растворе/смеси/сплаве; m – масса/объем вещества; M – масса/объем всей смеси/сплава/раствора. Принцип решения следующий:
, где K – процент вещества в растворе/смеси/сплаве; m – масса/объем вещества; M – масса/объем всей смеси/сплава/раствора. Принцип решения следующий:
1) Определить массу/объем всех смесей, о которых идет речь в задаче.
2) Определить массу/объем дополнительного вещества во всех смесях, о которых идет речь в задаче.
3) Определить процентное содержание дополнительного вещества во всех смесях, о которых идет речь в задаче.
4) Выбрать удобную величину и обозначить ее за x, а остальные величины выразить через x по формуле 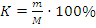 .
.
5) Получить ответ, решив уравнение или систему.
Пример: Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
Решение: для удобства можно составить таблицу:
| Объем раствора | Объем вещества | Процентное содержание | |
|
Раствор 1 |
4 л | 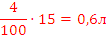 |
15% |
| Раствор 2 | 6 л | 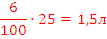 |
25% |
| Раствор 3 | 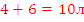 |
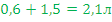 |
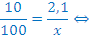 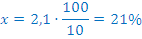 |
В таблице красным обозначены первичные расчеты по данным условия; зеленым – расчеты по данным, полученным в результате первичных расчетов. После того, как все возможные данные вычислены, искомый процент обозначен за x, составлена пропорция и получен ответ (выделено синим цветом).
Ответ: 21%.
Решение задач на движение
Можно выделить несколько типов наиболее распространенных задач на движение:
1) Движение по воде;
2) Движение по окружности;
3) Движение по прямой.
Здесь важно знать формулу равномерного движения: 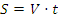 , где S – пройденный путь, V – скорость, t – время движения.
, где S – пройденный путь, V – скорость, t – время движения.
Пример: Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
Решение: за два часа скорый поезд проехал 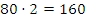 км, значит расстояние между поездами к этому моменту стало
км, значит расстояние между поездами к этому моменту стало 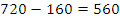 км. С этого момента поезда сближаются со скоростью
км. С этого момента поезда сближаются со скоростью 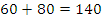 км/ч. Найдем время, через которое они встретятся:
км/ч. Найдем время, через которое они встретятся: 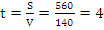 часа.
часа.
Ответ: 4 ч.
Решение задач на работу
В задачах на совместную работу весь объем работы, как правило, принимается за единицу.
Продуктивность (производительность, скорость) труда – это объем работы, который может быть выполнен в единицу времени.
Решение основано на формуле: 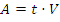 , где A – весь объем работы, t – время, за которое выполнена вся работа, V – продуктивность труда.
, где A – весь объем работы, t – время, за которое выполнена вся работа, V – продуктивность труда.
Пример: Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Решение: объем работы нужно принять за единицу. Тогда производительность труда каждого рабочего составляет: 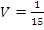 . Пусть время совместной работы x, при этом несложно догадаться, что совместная продуктивность труда равна суммарной продуктивности двух рабочих.
. Пусть время совместной работы x, при этом несложно догадаться, что совместная продуктивность труда равна суммарной продуктивности двух рабочих.
Согласно формуле: 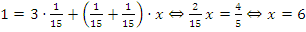 часов. Рабочие вместе работали 6 часов, кроме того первый работал еще три часа. Так, на выполнение заказа ушло 3+6=9 часов.
часов. Рабочие вместе работали 6 часов, кроме того первый работал еще три часа. Так, на выполнение заказа ушло 3+6=9 часов.
Ответ: 9 ч.
Краткий конспект подготовки к ЗНО по математике №10 Система координат на плоскости. Оси. Координаты точки. Графики простейших функций
Урок 10. Система координат на плоскости. Оси. Координаты точки. Графики простейших функций
Система координат xOy
Для того, чтобы прямая стала координатной осью, она должна иметь направление, точку начала отсчета и масштаб.
Прямоугольная (или декартова) система координат на плоскости задается парой взаимно перпендикулярных координатных осей: oX, направленной слева направо и oY, направленной снизу вверх, имеющих общее начало в точке O, и одинаковый масштаб.
Горизонтальная ось x называется осью абсцисс и имеет уравнение  . Вертикальная ось y называется осью ординат и имеет уравнение
. Вертикальная ось y называется осью ординат и имеет уравнение  .
.
Любой график функции, проходящий через точку с координатой  , где a – произвольное действительное число, пересекает ось абсцисс. Любой график функции, проходящий через точку с координатой
, где a – произвольное действительное число, пересекает ось абсцисс. Любой график функции, проходящий через точку с координатой  , где b – произвольное действительное число, пересекает ось ординат.
, где b – произвольное действительное число, пересекает ось ординат.
Наиболее распространенные функции, их графики и свойства
1)  – вертикальная и горизонтальная прямые соответственно.
– вертикальная и горизонтальная прямые соответственно.
Пример:  .
.

2)  – линейная функция (график – прямая линия).
– линейная функция (график – прямая линия).
Метод построения: «по точкам» – необходимо подставить вместо аргумента любые два числовые значения и вычислить какие при этом получаются значения функции. Для удобства полученные данные вносят в специальную табличку. Для построения прямой достаточно провести ее через две точки, нанесенные в системе координат.
Пример: 
Решение: подставим в функцию произвольные значения аргумента

Занесем значения в табличку:
| x | y |
| 0 | -1 |
| 1 | 1 |
Нанесем точки в системе координат и проведем через них график прямой: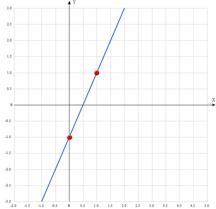
В зависимости от знаков коэффициентов можно определить, как проходит график линейной функции:
А.  : угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в положительном луче;
: угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в положительном луче;
Б.  : угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в положительном луче;
: угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в положительном луче;
В.  : угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в отрицательном луче;
: угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в отрицательном луче;
Г.  : угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в отрицательном луче.
: угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в отрицательном луче.
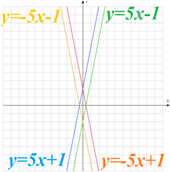
Вывод: коэффициент k отвечает за угол между положительным направлением оси абсцисс и прямой; коэффициент b отвечает за точку пересечения с осью ординат.
3)  – квадратичная функция (график – парабола).
– квадратичная функция (график – парабола).
Метод построения: «по вершине» (самый удобный) – необходимо вычислить координаты вершины параболы, а затем построить ее ветви с учетом их направления и пересечения осей координат.
Координаты вершины: 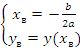
В зависимости от знаков коэффициентов можно охарактеризовать график, не выполняя построения.
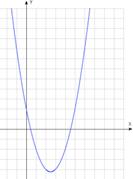
Коэффициент a отвечает за направление ветвей параболы. При  ветви направлены вверх, при
ветви направлены вверх, при  вниз.
вниз.
Коэффициент c отвечает за точку пересечения с осью ординат: при  парабола пересекает ось ординат в положительном луче; при
парабола пересекает ось ординат в положительном луче; при  проходит через начало координат; при
проходит через начало координат; при  – пересекает ось в отрицательном луче.
– пересекает ось в отрицательном луче.
Коэффициент b при определенном коэффициенте a задает положение вершины по оси абсцисс:
А. При  , вершина расположена в левой полуплоскости;
, вершина расположена в левой полуплоскости;
Б. При  , вершина расположена в правой полуплоскости;
, вершина расположена в правой полуплоскости;
В. При  , вершина расположена в правой полуплоскости;
, вершина расположена в правой полуплоскости;
Г. При  , вершина расположена в левой полуплоскости.
, вершина расположена в левой полуплоскости.
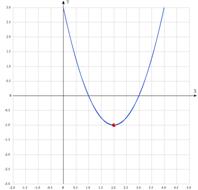
Пример: 
Решение: вычислим координаты вершины  . Построим параболу, ветви которой направлены вверх, т.к.
. Построим параболу, ветви которой направлены вверх, т.к. :
:
4) 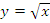 – функция квадратного корня.
– функция квадратного корня. 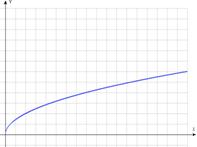
5)  – простейшая кубическая функция (график – кубическая парабола).
– простейшая кубическая функция (график – кубическая парабола).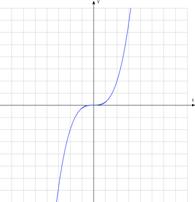
6)  – простейшая дробно-рациональная функция (график – гипербола).
– простейшая дробно-рациональная функция (график – гипербола).
В данном случае оси координат являются асимптотами графика функции  .
.
Асимптота – это прямая, к которой бесконечно близко приближается график функции, но никогда ее не достигает.
В простейшей гиперболе при стремлении аргумента к бесконечности график бесконечно прижимается к оси абсцисс, а при стремлении аргумента к нулю – к оси ординат, но гипербола никогда не пересекает осей.
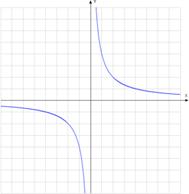
Кроме того, для графика функции  при
при  правая ветвь гиперболы расположена над осью абсцисс, а левая под осью; при
правая ветвь гиперболы расположена над осью абсцисс, а левая под осью; при  правая ветвь гиперболы расположена под осью абсцисс, а левая над осью.
правая ветвь гиперболы расположена под осью абсцисс, а левая над осью.
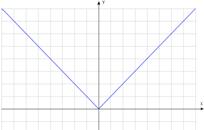
7)  – простейшая функция модуля.
– простейшая функция модуля.
Краткий конспект подготовки к ЗНО по математике №11 Уравнения с модулями. Системы уравнений
Урок 11. Уравнения с модулями. Системы уравнений
Решение уравнений, содержащих неизвестную под модулем
Уравнения, в которых переменная стоит под знаком модуля и такой модуль один, в простейшем случае сводятся к уравнениям вида  , где a – действительное число. Если
, где a – действительное число. Если  , то решений нет, если
, то решений нет, если  , то решение подобного уравнения:
, то решение подобного уравнения:
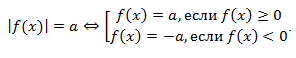
Пример:  .
.
Решение:
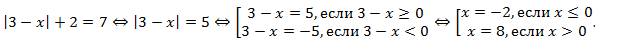
Ответ: -2;8.
Также уравнение с одним модулем может иметь вид  . Решение такого уравнения аналогично.
. Решение такого уравнения аналогично.
Пример: 
Решение:
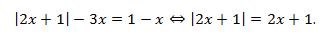
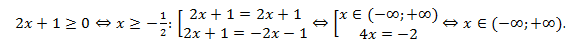
Объединив решение с ограничением на правую часть уравнения, получаем
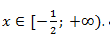
Ответ: 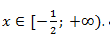 .
.
При решении уравнений с несколькими модулями вида нужно придерживаться алгоритма:
нужно придерживаться алгоритма:
Определить нули подмодульных выражений, решив уравнения:  и т.д.;
и т.д.;
Разбить множество значений аргумента на интервалы определенными в п.1 нулями;
Определить знаки подмодульных выражений на каждом интервале;
Рассмотреть решение уравнения на каждом интервале отдельно, раскрыв модули с учетом знаков подмодульных выражений.
Пример:  .
.
Решение: 1. Определяем нули: 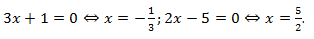
2. Множество значений аргумента разбито на интервалы:  .
.
3. Определяем знаки подмодульных выражений:
4. Рассмотрим решение уравнения для трех случаев.
При  :
: 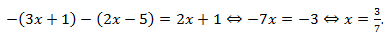 . Найденный корень не входит в рассматриваемый интервал.
. Найденный корень не входит в рассматриваемый интервал.
При  :
: 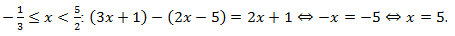 Найденный корень не входит в рассматриваемый интервал.
Найденный корень не входит в рассматриваемый интервал.
При  :
: 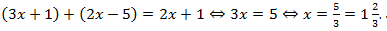 . Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.
. Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.
Ответ: корней нет.
Системы линейных уравнений
Система вида 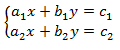 называется системой линейных уравнений с двумя переменными, здесь
называется системой линейных уравнений с двумя переменными, здесь  – действительные числа. Решить систему означает найти все пары значений
– действительные числа. Решить систему означает найти все пары значений  , которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.
, которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.
1. Метод подстановки.
Заключается в том, что в одном из уравнений системы нужно выразить одну переменную через другую и подставить полученное выражение во второе уравнение системы.
Пример:
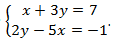
Решение:
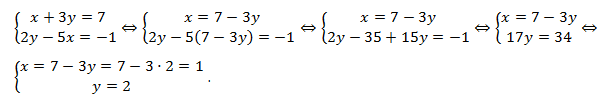
Ответ: (1;2).
2. Метод алгебраического сложения.
Заключается в том, что нужно получить противоположные коэффициенты при одной из переменных уравнения и сложить уравнения, при этом избавившись от одной переменной. Таким образом, решение системы сводится к решению линейного уравнения с одной переменной.
Пример:
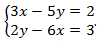
Решение:
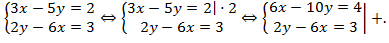
Получаем
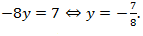
Ответ:  .
.
3. Графический метод.
Заключается в построении графиков двух линейных функций. Если прямые пересеклись – координаты точки пересечения будут единственным решением системы. Если прямые параллельны или совпали, то система не имеет решений или, соответственно, имеет бесконечно много решений.
Количество решений системы линейных уравнений
Система двух линейных уравнений с графической точки зрения представляет собой две прямые, построенные в системе координат. Две прямые могут пересекаться только в одной точке. Также они могут совпадать или быть параллельными. Очевидно, что система двух линейных уравнений имеет только три варианта решения:
Единственное решение (прямые пересекаются);
Нет решений (прямые параллельны);
Бесконечно много решений (прямые совпали).
Для системы 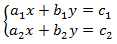 существует простой способ определить наличие решений:
существует простой способ определить наличие решений:
– если  , то система имеет бесконечное количество решений;
, то система имеет бесконечное количество решений;
– если  , то система не имеет решений;
, то система не имеет решений;
– если  , то система имеет одно решение.
, то система имеет одно решение.
Системы уравнений высших степеней
Системы, в которых одно из уравнений линейное, как правило, решаются методом подстановки. Если в системе оба уравнения нелинейные, то применяют также комбинирование уравнений с целью получения нового уравнения, которое можно разложить на простые множители.
Пример: 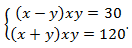
Решение: Нужно раскрыть скобки: 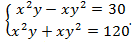 Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания:
Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания: 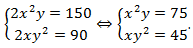 Нужно умножить уравнения системы:
Нужно умножить уравнения системы: 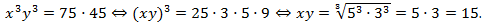 Теперь можно применить способ подстановки:
Теперь можно применить способ подстановки: 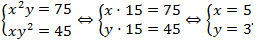
Ответ: 5;3.
Краткий конспект подготовки к ЗНО по математике №9 "Рациональные уравнения. Уравнения высших степеней"
Урок 9. Рациональные уравнения. Уравнения высших степеней
Понятие ОДЗ
Областью допустимых значений (ОДЗ) алгебраического выражения называют множество всех допустимых совокупностей значений букв, входящих в это выражение.
В частности знаменатель дроби не может быть равен нулю, поэтому значения переменных, при которых знаменатель равен нулю, недопустимы – не входят в ОДЗ
Пример: найти ОДЗ выражения  .
.
Решение: знаменатели обеих дробей не могут быть равны нулю, имеем систему:
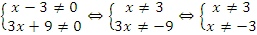
Ответ: x≠±3.
Решение уравнений вида 
Произведение выражений равно нулю тогда и только тогда, когда одно из них равно нулю, а остальные при этом существуют. Поэтому уравнение вида  заменяется совокупностью уравнений:
заменяется совокупностью уравнений:
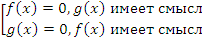
Пример: решить уравнение  .
.
Решение: 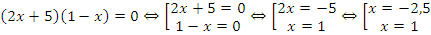
Ответ: -2,5;1.
Решение уравнений вида 
Дробь равна нулю тогда и только тогда, когда числитель ее равен нулю, а знаменатель при этом не равен нулю. Поэтому уравнения вида  заменяются совокупностью:
заменяются совокупностью: 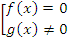
Пример: решить уравнение  .
.
Решение: 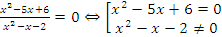
Корни квадратных уравнений определяем по теореме Виета: 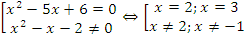 .
.
Ответ: 3.
Уравнения высших степеней. Метод замены переменных
Если в уравнении содержится переменная, степень которой выше 2, то такое уравнение называется уравнением высшей степени. Для решения уравнений высших степеней существует несколько наиболее распространенных методов:
1) Метод замены переменных;
2) Подбора корней;
3) Разложения на множители.
Метод замены переменных
Пример: решить уравнение 
Решение: очевидна замена переменных:  .
.
Получается уравнение:  . Согласно теореме Виета его корни:
. Согласно теореме Виета его корни:
В исходных переменных: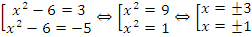
Ответ: ±1; ±3.
Пример: решить уравнение  .
.
Решение: нужно сгруппировать крайние и средние скобки: ⇔
⇔ .
.
Можно заметить, что удобна замена:  , тогда получим уравнение
, тогда получим уравнение  ⇔
⇔ ⇔
⇔ . Согласно теореме Виета корни уравнения:
. Согласно теореме Виета корни уравнения:  .
.
В исходных переменных: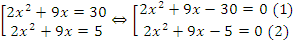
Дискриминанты уравнений: .
.
Корни первого уравнения: 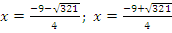 .
.
Корни второго уравнения:  .
.
Ответ: 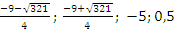 .
.
Замечание: метод подбора корней интуитивно понятен, а метод разложения на множители не требует примеров, т.к. разложение выражений на множители и решение уравнений вида  уже изучалось.
уже изучалось.
Биквадратные уравнения
Уравнение вида  называется биквадратным. Такие уравнения решаются приведением к квадратному уравнению с помощью замены вида
называется биквадратным. Такие уравнения решаются приведением к квадратному уравнению с помощью замены вида  .
.
Пример: решить уравнение .
.
Решение: согласно правилу выполним замену  , тогда:
, тогда:  .
.
В исходных переменных: 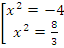 . Первое уравнение не имеет смысла, второе уравнение имеет два корня
. Первое уравнение не имеет смысла, второе уравнение имеет два корня 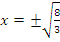 .
.
Ответ: 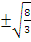 .
.
Тесты подготовки к ЗНО:
Онлайн-тест подготовки к ЗНО по математике №9 "Рациональные уравнения. Уравнения высших степеней"
Краткий конспект подготовки к ЗНО по математике №8 "Линейные уравнения. Квадратные уравнения"
Урок 8. Линейные уравнения. Квадратные уравнения
Равенства и их свойства, уравнение с одной переменной
Свойства равенств:
1) К обеим частям равенства можно прибавить или отнять любое численное выражение, имеющее смысл, при этом равенство не изменится:  ;
;
2) Обе части равенства можно умножить или разделить (кроме нуля) на любое численное выражение, имеющее смысл, при этом равенство не изменится:  ;
;
3) Обе части равенства можно возвести в одну и ту же нечетную степень, при этом равенство не изменится:  ;
;
4) Обе части равенства (если они обе положительны) можно возвести в одну и ту же четную степень, при этом равенство не изменится:  .
.
Равенство, содержащее одну переменную ( ), называется уравнением с одной переменной. Корнем уравнения называется такое значение переменной, при котором выражение обращается в верное числовое равенство. Решить уравнение означает найти все его корни или доказать, что корней нет.
), называется уравнением с одной переменной. Корнем уравнения называется такое значение переменной, при котором выражение обращается в верное числовое равенство. Решить уравнение означает найти все его корни или доказать, что корней нет.
Уравнения, имеющие одинаковые корни, называются равносильными.
Равносильные преобразования уравнений:
В уравнении можно перенести любое слагаемое из одной части в другую, сменив его знак на противоположный:  ⇔
⇔ ;
;
Обе части уравнения можно умножить или разделить на любое отличное от нуля число:  ⇔
⇔ .
.
Линейные уравнения
Уравнение вида  и все, которые к нему сводятся, называются линейными уравнениями с одной переменной. Здесь
и все, которые к нему сводятся, называются линейными уравнениями с одной переменной. Здесь  – произвольные действительные числа,
– произвольные действительные числа,  – переменная; коэффициент
– переменная; коэффициент  называют коэффициентом при переменной, коэффициент
называют коэффициентом при переменной, коэффициент  – свободным членом.
– свободным членом.
Линейное уравнение может содержать множество подобных слагаемых, в таком случае его сначала необходимо свести к простейшему виду, а затем решить.
При решении линейных уравнений есть три случая:
1) a≠0: в таком случае уравнение имеет единственный корень  ;
;
2) a=0,b=0: в этом случае уравнение превращается в равенство  , что верно при любом действительном
, что верно при любом действительном  , поэтому имеет бесчисленное множество решений;
, поэтому имеет бесчисленное множество решений;
3)a=0,b≠0: в этом случае имеем равенство  ≠
≠ , что неверно ни при каком значении
, что неверно ни при каком значении  и уравнение не имеет решений.
и уравнение не имеет решений.
Пример: решить уравнение  ⇔
⇔ ⇔
⇔ ⇔
⇔ .
.
Уравнения, которые сводятся к линейным
Пример: решить уравнение  .
.
Решение:  ⇔
⇔ ⇔
⇔ ⇔
⇔ ⇔
⇔ ⇔
⇔
Ответ: -23/17.
Пример: решить уравнение .
.
Решение:  ⇔
⇔ ⇔
⇔ ⇔
⇔
⇔ ⇔
⇔ .
.
Ответ: -12/7.
Неполные квадратные уравнения
Уравнение вида  называется квадратным. Здесь
называется квадратным. Здесь  – действительные числа,
– действительные числа,  – переменная.
– переменная.
Квадратное уравнение может быть неполным, если один из коэффициентов  равен нулю, или оба они равны нулю:
равен нулю, или оба они равны нулю:  ;
;  ;
;  .
.
Решение неполных квадратных уравнений:
Нужно разложить левую часть на множители:  . Произведение равно нулю только тогда, когда один из множителей равен нулю, а остальные при этом существуют:
. Произведение равно нулю только тогда, когда один из множителей равен нулю, а остальные при этом существуют: 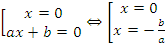
 .
.
Разделим уравнение на коэффициент при  . Согласно свойствам квадратичной функции, левая часть может принимать только неотрицательные значения, поэтому:
. Согласно свойствам квадратичной функции, левая часть может принимать только неотрицательные значения, поэтому: 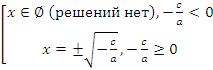
 .
.
Данное уравнение имеет единственное решение  . Обратим внимание, что коэффициент a мы считаем ненулевым.
. Обратим внимание, что коэффициент a мы считаем ненулевым.
Пример: решить уравнение  .
.
Решение:
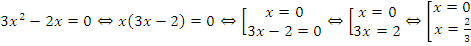
Ответ: 0; 2/3.
Дискриминант
Для поиска корней полного квадратного уравнения введено понятие дискриминанта. Это выражение вида:  , где
, где  – коэффициенты квадратного уравнения.
– коэффициенты квадратного уравнения.
В зависимости от значения дискриминанта можно выяснить наличие корней у квадратного уравнения:
1) D>0: уравнение имеет два различных корня, которые определяются по формуле 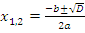 .
.
Отметим, что если коэффициент  кратен четырем, имеет место формула:
кратен четырем, имеет место формула:
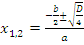 .
.
2) D=0: уравнение имеет два совпадающих корня, но принято говорить – уравнение имеет один корень  .
.
3) D<0: уравнение не имеет корней.
Пример: решить уравнение  .
.
Решение: Находим дискриминант:  . Дискриминант положителен – уравнение имеет два корня:
. Дискриминант положителен – уравнение имеет два корня:
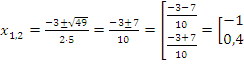
Ответ: -1;0,4.
Теорема Виета
Пусть задано произвольное квадратное уравнение: 
Прямая теорема Виета – сумма корней приведенного квадратного уравнения равна коэффициенту при  , взятому с противоположным знаком, а произведение корней равно свободному члену:
, взятому с противоположным знаком, а произведение корней равно свободному члену: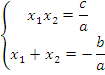
Обратная теорема Виета – если верно, что 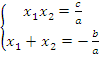 , то
, то  и
и  являются корнями квадратного уравнения:
являются корнями квадратного уравнения:  .
.
Замечание: все квадратные уравнения можно решать с использованием дискриминанта, другие способы применяются из соображений ускорения процесса решения.
Пример: найти корни уравнения, не решая его:  .
.
Решение: согласно прямой теореме Виета: 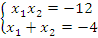 . Методом подбора определяем:
. Методом подбора определяем:  .
.
Ответ: 2;-6.
Разложение квадратного трехчлена на множители
Если квадратное уравнение  имеет корни
имеет корни  и
и  , то квадратный трехчлен
, то квадратный трехчлен  раскладывается на множители следующим образом:
раскладывается на множители следующим образом:
Пример: разложить на множители  .
.
Решение: рассмотрим квадратное уравнение:  . Согласно теореме Виета его корни:
. Согласно теореме Виета его корни:  . Тогда имеем разложение:
. Тогда имеем разложение:  .
.
Ответ:  .
.
Тесты подготовки к ЗНО:
Онлайн-тест подготовки к ЗНО по математике №8 "Линейные уравнения. Квадратные уравнения"
Краткий конспект подготовки к ЗНО по математике №6 "Корень n-ной степени из действительного числа. Обобщение понятия степени"
Урок 6. Корень n-ной степени из действительного числа. Обобщение понятия степени
Понятие и свойства корня n-ной степени из действительного числа
Корнем  -ой степени из действительного числа a(
-ой степени из действительного числа a( 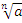 ) называется такое число
) называется такое число  , что:
, что: 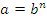 , где
, где 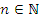 .
.
Для чётных значений  ≥0.
≥0.
Для нечётных значений  такого ограничения нет.
такого ограничения нет.
Для четных  используют понятие арифметического корня из числа
используют понятие арифметического корня из числа  , это неотрицательное число,
, это неотрицательное число,  -ная степень которого равна
-ная степень которого равна  .
.
Пример: арифметический квадратный корень из 16 равен 4, квадратный корень из 16 это ±4.
Свойства корня:
1) 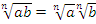 (a,b≥0 при чётном n).
(a,b≥0 при чётном n).
2) 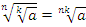 (a≥0 при чётном n или k).
(a≥0 при чётном n или k).
3) 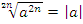
4) 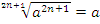
5) 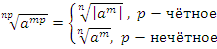
Вынесение и внесение множителя под знак корня
Чтобы вынести множитель из-под знака корня, необходимо подкоренное выражение представить в виде степени или произведения степеней с показателем, кратным показателю корня.
Пример:
1) 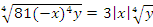 ;
; 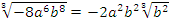 ;
; 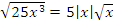
Чтобы внести множитель под знак корня, нужно возвести его в степень корня и после этого внести.
Пример:
1) 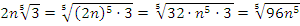 ;
; 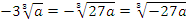 ;
; 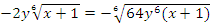 (вносить минус под корень четной степени нельзя).
(вносить минус под корень четной степени нельзя).
Избавление от иррациональности в знаменателе
Чтобы избавиться от иррациональности в знаменателе дроби, нужно всю дробь домножить на выражение, сопряженное к знаменателю. Основные ситуации, которые могут встретиться:
1) Если в знаменателе стоит корень, который не входит в слагаемые, то числитель и знаменатель дроби нужно домножить на другой корень так, чтобы в результате этот корень можно было извлечь до целого выражения.
Пример: 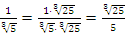
2) Если в знаменателе стоит сумма или разность двух выражений и хотя бы одно из них содержит квадратный корень, нужно домножить на сопряжённое выражение – такое же выражение, но с противоположным знаком.
Пример: 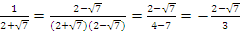
Принцип «исчезновения» иррациональности основан на применении формулы разности квадратов.
3) Если в знаменателе стоит сумма или разность двух выражений и хотя бы одно из них содержит кубический корень, нужно домножить на неполный квадрат разности или суммы этих выражений – чтобы знаменатель свернуть по формуле суммы или разности кубов соответственно.
Пример: 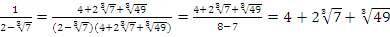
Иррациональные выражения
Алгебраическое выражение называется иррациональным, если в нём присутствует операция извлечения корня из переменной.
Пример: упростить выражение 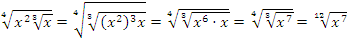
Степень действительного числа с рациональным показателем
Ранее была рассмотрена степень с натуральным показателем и степень с отрицательным показателем. Степень с дробным (рациональным) показателем соответствует корню: 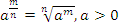
Для степени с дробным показателем справедливы все свойства степени с натуральным и отрицательным показателем. Так, теперь степень с неотрицательным основанием a определена для любого рационального показателя.
Пример: 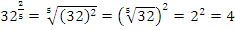
Пример: упростить выражение
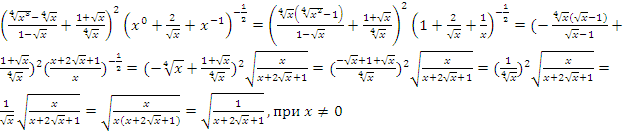
Тесты подготовки к ЗНО:
Онлайн-тест подготовки к ЗНО по математике №6 "Корень n-ной степени. Работа с иррациональными выражениями"
Онлайн-тест подготовки к ЗНО по математике №7 "Итоговый контроль. Обобщение"
Краткий конспект подготовки к ЗНО по математике №7 "Итоговая контрольная работа по преобразованиям"
Урок 7. Итоговая контрольная работа по преобразованиям
Пример 1: вычислить
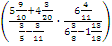
Решение: сначала нужно определить порядок действий:
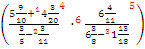
1. Сложение дробей:
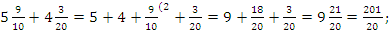
2-3. Вычитание дробей:
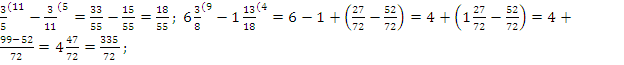
4-5. Деление дробей:
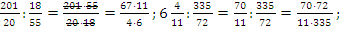
6. Умножение дробей:
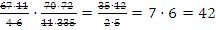
Ответ: 42.
Пример 2: упростить выражение
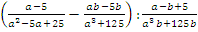
Решение: сначала нужно выполнить вычитание в скобках, для этого привести дроби к общему знаменателю с помощью ФСУ. 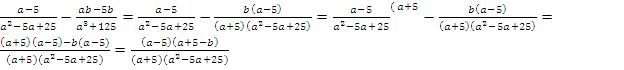
Теперь нужно разделить дроби:
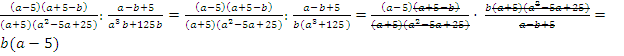
Ответ:  .
.
Пример 3: вычислить
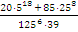
Решение: нужно во всех слагаемых выделить пятерку в максимальной степени, для этого разложить на простые множители:
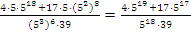
Теперь можно вынести в числителе общий множитель и сократить дробь:
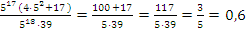
Ответ: 0,6.
Пример 4: вычислить значение выражения
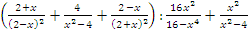 при x=12.
при x=12.
Решение: сначала нужно выполнить сложение в скобках, для этого привести дроби к общему знаменателю с помощью ФСУ.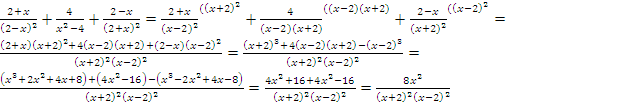
Теперь нужно разделить дроби:
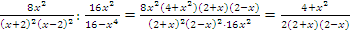
Осталось сложить дроби:
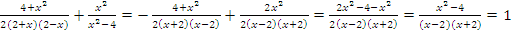
Как видим получилось численное значение, и подставлять значение переменной нет необходимости.
Ответ: 1.
Пример 5: вычислить
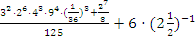
Решение:
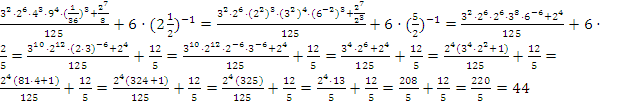
Ответ: 44.
Тесты подготовки к ЗНО:
Онлайн-тест подготовки к ЗНО по математике №7 "Итоговый контроль. Обобщение"
Краткий конспект подготовки к ЗНО по математике №4-5 "Дробно-рациональные выражения. Формулы сокращенного умножения."
Урок 4-5. Дробно-рациональные выражения. Формулы сокращенного умножения
Формулы сокращенного умножения
Очень часто при разложении многочленов на множители применяются формулы сокращенного умножения. Вот наиболее важные из них:
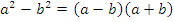
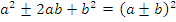
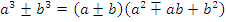
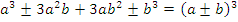
Сокращение рациональных дробей
Дробь, в числителе и знаменателе которой стоят многочлены, называется рациональной.
Чтобы сократить рациональную дробь, нужно ее числитель и знаменатель разложить на множители. При сокращении следует учитывать, что на ноль делить нельзя, поэтому нужно накладывать ограничения на значения переменных.
ОДЗ – область допустимых значений – это все те значения, которые могут принимать переменные, входящие в выражение, и при которых данное выражение имеет смысл.
Пример: сократить дробь
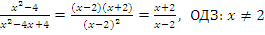
.
Действия с рациональными дробями
Все действия с рациональными дробями выполняются аналогично обыкновенным дробям, т.е. рациональные дроби точно так же можно складывать, вычитать, умножать, делить и возводить в степень.
Для сложения/вычитания рациональных дробей их нужно привести к общему знаменателю – для этого знаменатели исходных дробей нужно разложить на множители.
Пример: вычесть дроби
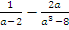 .
.
Решение:
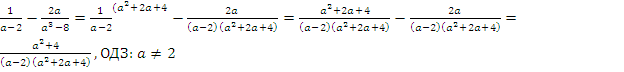
Ответ:
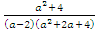 .
.
Умножать и делить можно любые рациональные дроби, правила такие же, как для обыкновенных дробей: 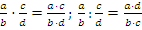
при этом вместо  могут стоять любые многочлены. После того, как дроби записаны под общей дробной чертой, все многочлены нужно разложить на множители и максимально сократить.
могут стоять любые многочлены. После того, как дроби записаны под общей дробной чертой, все многочлены нужно разложить на множители и максимально сократить.
Чтобы возвести рациональную дробь в степень, нужно возвести в степень и ее числитель, и знаменатель.
Пример:
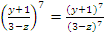 .
.
Тождественные преобразования с дробями
Пример: упростить 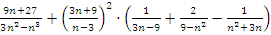 .
.
Решение:
1) Нужно привести дроби в скобках к общему знаменателю и выполнить действия. Числитель и знаменатель второй дроби домножим на (-1), чтобы все множители знаменателей стали однотипными: 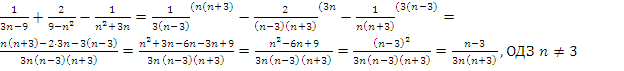
2) Выполним умножение:
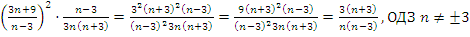
3) Выполним сложение. Для этого приведем дроби к общему знаменателю:
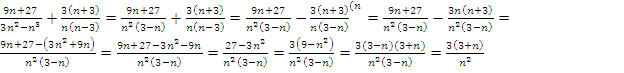
Ответ: 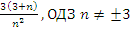
Пример: упростить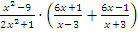
Решение:
1) Выполним сложение в скобках, для этого приведем дроби к общему знаменателю:
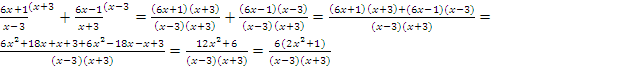
2) Умножим дроби:
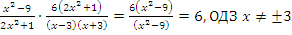
Ответ: 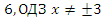 .
.
Доказательство тождеств
Пример: доказать тождество
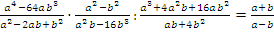 .
.
Доказательство: разложим все многочлены в левой части на множители: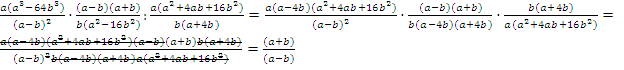
Тождество доказано.
Тесты подготовки к ЗНО:
Онлайн-тест подготовки к ЗНО по математике №4 "Дробные рациональные выражения. Формулы сокращённого умножения."
Онлайн-тест подготовки к ЗНО по математике №5 "Дробно-рациональные выражения. Формулы сокращённого умножения"
Страница 1 из 2