Краткий конспект подготовки к ЗНО по математике №14-15 Линейные неравенства. Квадратичные неравенства. Метод интервалов при решении неравенств

Урок 14-15. Линейные неравенства. Квадратичные неравенства. Метод интервалов при решении неравенств

Линейные неравенства

Символическая запись, в которой два числа или выражения, содержащие переменные, связаны знаком «больше» (>) или «меньше» (<), называется неравенством. Наряду со строгими неравенствами (а>b) рассматривают и нестрогие неравенства: а≥b.
Свойства неравенств:
1. Если a>b и b>с, то a>с.
2. Если a>b, то a+с>b+с, с – любое число.
3. Если a>b и с>d, то a+с>b+d. Неравенства одинакового смысла можно почленно складывать.
4. Если a,b,с,d — положительные числа и a>b,с>d, то aс >bd. Неравенства одинакового смысла можно почленно умножать (с учетом знаков).
5. Если a>b ,с<d, то a-с>b-d. Неравенства противоположного смысла можно почленно вычитать, оставляя знак первого неравенства.

Решить неравенство с одной переменной – значит найти все его решения, то есть значения переменной, при которых неравенство истинно, или доказать, что их нет.
Правила решения неравенств:
1) Любое слагаемое неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.
2) Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
3) Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Пример: ⇔⇔⇔

Системы и совокупности линейных неравенств

Если неравенства объединены в систему, то решением системы будут те значения переменных, которые удовлетворяют одновременно всем неравенствам. Решение системы соответствует пересечению решений всех неравенств.
Если неравенства объединены в совокупность, то решением ее будут те значения переменных, которые удовлетворяют хотя бы одному из неравенств совокупности. Решение совокупности соответствует объединению решений всех неравенств.

Квадратичные неравенства

Неравенства вида >(<;≥;≤)0 называются квадратичными. Здесь a,b,c – любые действительные числа, a≠0. Есть несколько случаев решения квадратичных неравенств:
1)  ветви параболы направлены вверх, квадратное уравнение имеет два корня. Внутри интервала корней значения квадратного трехчлена отрицательны, вне интервала корней – положительны, в корнях квадратный трехчлен обращается в ноль;

2)  ветви параболы направлены вверх, квадратное уравнение имеет один корень. Значения квадратного трехчлена положительны при всех значениях аргумента, кроме корня – здесь квадратный трехчлен обращается в ноль;
3)  ветви параболы направлены вверх, квадратное уравнение не имеет корней. Значения квадратного трехчлена положительны при всех значениях аргумента;
4)  ветви параболы направлены вниз, квадратное уравнение имеет два корня. Внутри интервала корней значения квадратного трехчлена положительны, вне интервала корней – отрицательны, в корнях квадратный трехчлен обращается в ноль;
5) ветви параболы направлены вниз, квадратное уравнение имеет один корень. Значения квадратного трехчлена отрицательны при всех значениях аргумента, кроме корня – здесь квадратный трехчлен обращается в ноль;
6)  ветви параболы направлены вниз, квадратное уравнение не имеет корней. Значения квадратного трехчлена отрицательны при всех значениях аргумента.

Решение рациональных неравенств методом интервалов

Пример: ≥0
Решение: При решении примера будет сформулирован общий алгоритм решения неравенств методом интервалов. Он относится и к неравенствам с многочленами и к рациональным неравенствам. Чтобы пользоваться указанным алгоритмом, неравенство изначально следует привести к виду, когда по одну сторону некое выражение, а по другую ноль.
1. Найти нули функции: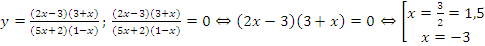
2. Определить ОДЗ: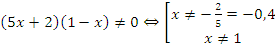 
3. Разбить область значений аргумента на интервалы нулями функции и точками разрыва ОДЗ. Точки, которые будут входить в решение неравенства обозначаются закрашенными, а которые не будут входить – выколотыми.
Точки расставляют по следующему принципу:
– закрашенные точки ставятся для нулей функции, если неравенство нестрогое;
– выколотые точки ставятся для нулей функции, если неравенство было строгое, и для точек разрыва ОДЗ функции.
В нашем случае мы поставим на оси координат выколотые точки для x=-0,4 и x=1, а закрашенные для x=1,5 и x=-3.
4. Определить знак функции на каждом интервале.
Для определения знаков есть два способа:
– брать на каждом интервале пробную точку, подставлять ее в функцию и определять знак – такой знак функция будет сохранять на всем интервале;
– с помощью пробной точки определить знак на крайнем правом интервале, а далее чередовать знаки при переходе через точки нулей функции и разрывов ОДЗ. Такой подход верен только при отсутствии множителей в четных степенях и модулей в неравенстве. Следует знать, что если какой-то множитель имеет четную степень, например, функция содержит множитель , то при переходе через точку x=2 знак функции сохраняется.
Для обозначения знаков промежутков удобно изображать характерную «змейку», которая рисуется над осью координат для положительных значений и под осью для отрицательных значений функции.
В нашем случае проверим, к примеру, знак функции в точке 10 для простоты расчетов: – функция на крайнем правом интервале отрицательна.
Далее на каждом из интервалов просто чередуем знаки функции, т.к. нет множителей в четных степенях и модулей.

5. Выписать в ответ объединение промежутков, которые соответствуют знаку неравенства, т.е. если в неравенстве интересуют значения больше нуля, то выписать промежутки с положительными значениями, и аналогично для других вариантов. Здесь важно помнить о том, что выколотые точки не входят в решение неравенства, а закрашенные точки входят.
Ответ: x∈[-3; -0,4)∪(1;1,5].

Неравенства с модулем
При решении модульных неравенств необходимо учитывать условия раскрывания модулей, а в остальном они решаются как обычные неравенства.
Пример: решить неравенство:.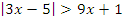
Решение: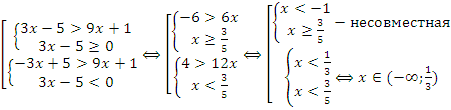

Ответ: x∈(-∞;1/3).