Краткий конспект подготовки к ЗНО по математике №8 "Линейные уравнения. Квадратные уравнения"

Урок 8. Линейные уравнения. Квадратные уравнения

Равенства и их свойства, уравнение с одной переменной

Свойства равенств:
1) К обеим частям равенства можно прибавить или отнять любое численное выражение, имеющее смысл, при этом равенство не изменится: ;
2) Обе части равенства можно умножить или разделить (кроме нуля) на любое численное выражение, имеющее смысл, при этом равенство не изменится: ;
3) Обе части равенства можно возвести в одну и ту же нечетную степень, при этом равенство не изменится: ;
4) Обе части равенства (если они обе положительны) можно возвести в одну и ту же четную степень, при этом равенство не изменится: .
Равенство, содержащее одну переменную (), называется уравнением с одной переменной. Корнем уравнения называется такое значение переменной, при котором выражение обращается в верное числовое равенство. Решить уравнение означает найти все его корни или доказать, что корней нет.
Уравнения, имеющие одинаковые корни, называются равносильными.
Равносильные преобразования уравнений:
В уравнении можно перенести любое слагаемое из одной части в другую, сменив его знак на противоположный: ⇔;
Обе части уравнения можно умножить или разделить на любое отличное от нуля число: ⇔.

Линейные уравнения

Уравнение вида  и все, которые к нему сводятся, называются линейными уравнениями с одной переменной. Здесь  – произвольные действительные числа,  – переменная; коэффициент  называют коэффициентом при переменной, коэффициент  – свободным членом.
Линейное уравнение может содержать множество подобных слагаемых, в таком случае его сначала необходимо свести к простейшему виду, а затем решить.
При решении линейных уравнений есть три случая:
1) a≠0: в таком случае уравнение имеет единственный корень ;
2) a=0,b=0: в этом случае уравнение превращается в равенство , что верно при любом действительном , поэтому имеет бесчисленное множество решений;
3)a=0,b≠0: в этом случае имеем равенство ≠, что неверно ни при каком значении  и уравнение не имеет решений.
Пример: решить уравнение ⇔⇔⇔.

Уравнения, которые сводятся к линейным

Пример: решить уравнение .
Решение: ⇔⇔⇔⇔⇔

Ответ: -23/17.
Пример: решить уравнение.
Решение: ⇔⇔⇔

⇔⇔.
Ответ: -12/7.

Неполные квадратные уравнения

Уравнение вида  называется квадратным. Здесь  – действительные числа,  – переменная.
Квадратное уравнение может быть неполным, если один из коэффициентов  равен нулю, или оба они равны нулю: ; ; .
Решение неполных квадратных уравнений:

Нужно разложить левую часть на множители: . Произведение равно нулю только тогда, когда один из множителей равен нулю, а остальные при этом существуют: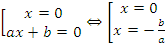 

.
Разделим уравнение на коэффициент при . Согласно свойствам квадратичной функции, левая часть может принимать только неотрицательные значения, поэтому: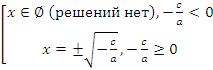 
.
Данное уравнение имеет единственное решение . Обратим внимание, что коэффициент a мы считаем ненулевым.
Пример: решить уравнение .
Решение:

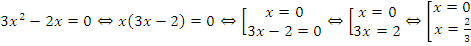
Ответ: 0; 2/3.

Дискриминант

Для поиска корней полного квадратного уравнения введено понятие дискриминанта. Это выражение вида: , где  – коэффициенты квадратного уравнения.
В зависимости от значения дискриминанта можно выяснить наличие корней у квадратного уравнения:
1) D>0: уравнение имеет два различных корня, которые определяются по формуле .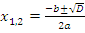

Отметим, что если коэффициент  кратен четырем, имеет место формула:

.
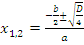2) D=0: уравнение имеет два совпадающих корня, но принято говорить – уравнение имеет один корень .
3) D<0: уравнение не имеет корней.
Пример: решить уравнение .
Решение: Находим дискриминант: . Дискриминант положителен – уравнение имеет два корня: 

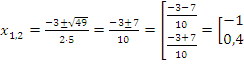
Ответ: -1;0,4.

Теорема Виета

Пусть задано произвольное квадратное уравнение:  
Прямая теорема Виета – сумма корней приведенного квадратного уравнения равна коэффициенту при , взятому с противоположным знаком, а произведение корней равно свободному члену: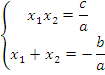

Обратная теорема Виета – если верно, что 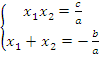, то  и  являются корнями квадратного уравнения: .
Замечание: все квадратные уравнения можно решать с использованием дискриминанта, другие способы применяются из соображений ускорения процесса решения.
Пример: найти корни уравнения, не решая его: .
Решение: согласно прямой теореме Виета: 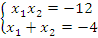. Методом подбора определяем: .
Ответ: 2;-6.

Разложение квадратного трехчлена на множители

Если квадратное уравнение  имеет корни  и , то квадратный трехчлен  раскладывается на множители следующим образом:

Пример: разложить на множители .
Решение: рассмотрим квадратное уравнение: . Согласно теореме Виета его корни: . Тогда имеем разложение: .
Ответ: .

Тесты подготовки к ЗНО:

Онлайн-тест подготовки к ЗНО по математике №8 "Линейные уравнения. Квадратные уравнения"