Краткий конспект подготовки к ЗНО по математике №10 Система координат на плоскости. Оси. Координаты точки. Графики простейших функций
Урок 10. Система координат на плоскости. Оси. Координаты точки. Графики простейших функций
Система координат xOy
Для того, чтобы прямая стала координатной осью, она должна иметь направление, точку начала отсчета и масштаб.
Прямоугольная (или декартова) система координат на плоскости задается парой взаимно перпендикулярных координатных осей: oX, направленной слева направо и oY, направленной снизу вверх, имеющих общее начало в точке O, и одинаковый масштаб.
Горизонтальная ось x называется осью абсцисс и имеет уравнение  . Вертикальная ось y называется осью ординат и имеет уравнение
. Вертикальная ось y называется осью ординат и имеет уравнение  .
.
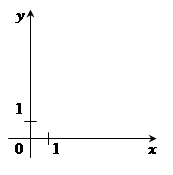
Любой график функции, проходящий через точку с координатой  , где a – произвольное действительное число, пересекает ось абсцисс. Любой график функции, проходящий через точку с координатой
, где a – произвольное действительное число, пересекает ось абсцисс. Любой график функции, проходящий через точку с координатой  , где b – произвольное действительное число, пересекает ось ординат.
, где b – произвольное действительное число, пересекает ось ординат.
Наиболее распространенные функции, их графики и свойства
1)  – вертикальная и горизонтальная прямые соответственно.
– вертикальная и горизонтальная прямые соответственно.
Пример:  .
.

2)  – линейная функция (график – прямая линия).
– линейная функция (график – прямая линия).
Метод построения: «по точкам» – необходимо подставить вместо аргумента любые два числовые значения и вычислить какие при этом получаются значения функции. Для удобства полученные данные вносят в специальную табличку. Для построения прямой достаточно провести ее через две точки, нанесенные в системе координат.
Пример: 
Решение: подставим в функцию произвольные значения аргумента

Занесем значения в табличку:
| x | y |
| 0 | -1 |
| 1 | 1 |
Нанесем точки в системе координат и проведем через них график прямой: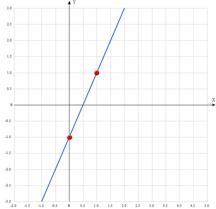
В зависимости от знаков коэффициентов можно определить, как проходит график линейной функции:
А.  : угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в положительном луче;
: угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в положительном луче;
Б.  : угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в положительном луче;
: угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в положительном луче;
В.  : угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в отрицательном луче;
: угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в отрицательном луче;
Г.  : угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в отрицательном луче.
: угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в отрицательном луче.
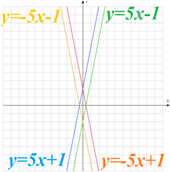
Вывод: коэффициент k отвечает за угол между положительным направлением оси абсцисс и прямой; коэффициент b отвечает за точку пересечения с осью ординат.
3)  – квадратичная функция (график – парабола).
– квадратичная функция (график – парабола).
Метод построения: «по вершине» (самый удобный) – необходимо вычислить координаты вершины параболы, а затем построить ее ветви с учетом их направления и пересечения осей координат.
Координаты вершины: 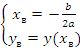
В зависимости от знаков коэффициентов можно охарактеризовать график, не выполняя построения.
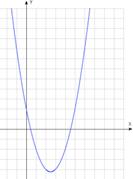
Коэффициент a отвечает за направление ветвей параболы. При  ветви направлены вверх, при
ветви направлены вверх, при  вниз.
вниз.
Коэффициент c отвечает за точку пересечения с осью ординат: при  парабола пересекает ось ординат в положительном луче; при
парабола пересекает ось ординат в положительном луче; при  проходит через начало координат; при
проходит через начало координат; при  – пересекает ось в отрицательном луче.
– пересекает ось в отрицательном луче.
Коэффициент b при определенном коэффициенте a задает положение вершины по оси абсцисс:
А. При  , вершина расположена в левой полуплоскости;
, вершина расположена в левой полуплоскости;
Б. При  , вершина расположена в правой полуплоскости;
, вершина расположена в правой полуплоскости;
В. При  , вершина расположена в правой полуплоскости;
, вершина расположена в правой полуплоскости;
Г. При  , вершина расположена в левой полуплоскости.
, вершина расположена в левой полуплоскости.
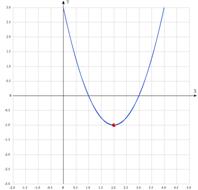
Пример: 
Решение: вычислим координаты вершины  . Построим параболу, ветви которой направлены вверх, т.к.
. Построим параболу, ветви которой направлены вверх, т.к. :
:
4) 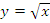 – функция квадратного корня.
– функция квадратного корня. 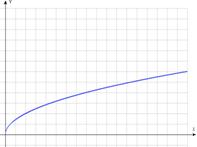
5)  – простейшая кубическая функция (график – кубическая парабола).
– простейшая кубическая функция (график – кубическая парабола).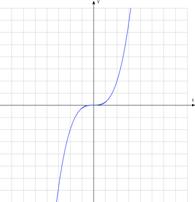
6)  – простейшая дробно-рациональная функция (график – гипербола).
– простейшая дробно-рациональная функция (график – гипербола).
В данном случае оси координат являются асимптотами графика функции  .
.
Асимптота – это прямая, к которой бесконечно близко приближается график функции, но никогда ее не достигает.
В простейшей гиперболе при стремлении аргумента к бесконечности график бесконечно прижимается к оси абсцисс, а при стремлении аргумента к нулю – к оси ординат, но гипербола никогда не пересекает осей.
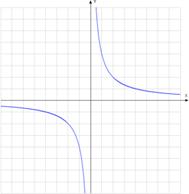
Кроме того, для графика функции  при
при  правая ветвь гиперболы расположена над осью абсцисс, а левая под осью; при
правая ветвь гиперболы расположена над осью абсцисс, а левая под осью; при  правая ветвь гиперболы расположена под осью абсцисс, а левая над осью.
правая ветвь гиперболы расположена под осью абсцисс, а левая над осью.
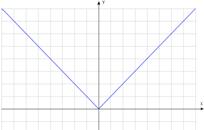
7)  – простейшая функция модуля.
– простейшая функция модуля.