Краткий конспект подготовки к ЗНО по математике №21-22 "Логарифмы. Логарифмические уравнения и неравенства"

Конспект 21-22. Логарифмы. Логарифмические уравнения и неравенства

Определение логарифма, основное логарифмическое тождество

Логарифмом числа b по основанию a (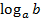) называют показатель степени, в которую нужно возвести число a, чтобы получить число b:
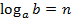, если 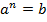, ОДЗ: a,b>0, a≠1.
Для удобства приняты сокращенные обозначения логарифмов, которые часто встречаются в разных областях науки:
1) Натуральным логарифмом (ln a) называют логарифм по основанию e≈2,7 – число Непера.
2) Десятичным логарифмом (lg a) называют логарифм по основанию 10.
Основное логарифмическое тождество: .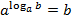
Это тождество следует из определения логарифма: так как логарифм – это показатель степени (n), то, возводя в эту степень число a, получим число b.

Свойства логарифмов

При условии, что a,b,c>0,a≠1:

1);

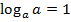2) ;

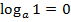3) 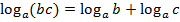 – логарифм произведения равен сумме логарифмов;

4) 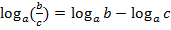 – логарифм частного равен разности логарифмов;

5) ;

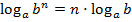6) ;

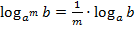7) ;

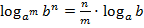8) 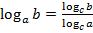 , c≠1 – переход к новому основанию логарифма;

9) 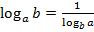 , b≠1.

Преобразование выражений, содержащих логарифмы

Пример: Вычислить .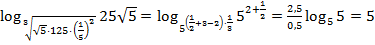
Пример: Вычислить .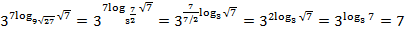
Пример: Вычислить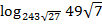, если .
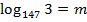Решение: .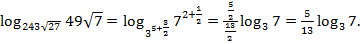
Теперь рассмотрим то, что дано по условию:

.
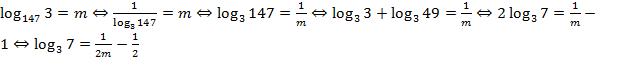Подставим это в исходное преобразованное выражение: .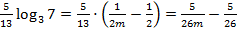
Ответ: .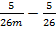

Основные методы решения логарифмических уравнений и неравенств

Простейшее логарифмическое уравнение имеет вид:
1) 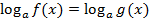, что соответствует простейшему уравнению f(x)=g(x) с учетом ОДЗ логарифмической функции;
2) 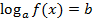, что решается по определению логарифма.
Логарифмическое уравнение любой сложности нужно преобразовать до простейшего.
При решении уравнений можно проверять полученные корни по ОДЗ либо выполнять подстановку.
1) Простейшие уравнения вида 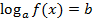 решаются по определению.
Пример: Решить .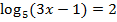
Решение: 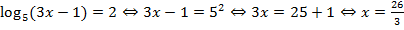. Выполним подстановку  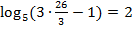– верное тождество.
Ответ: .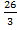

2) Уравнения вида .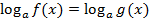
Пример: Решить .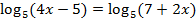
Решение: 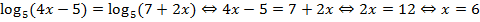. Подстановка  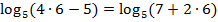– верное тождество.
Ответ: 6.

3) Уравнения вида 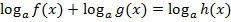 преобразовываются согласно свойствам 3 и 4.
Пример: Решить .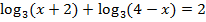
Решение:

.

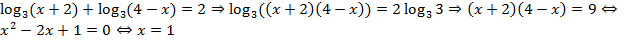Подстановка 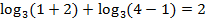 – верное тождество.
Ответ: 1.

4) Метод замены переменных. Логарифмические уравнения могут сводиться, например, к квадратным путем замены переменных
Пример: Решить .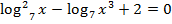
Решение: 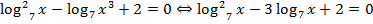. Удобно ввести замену: 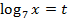, тогда: 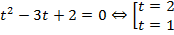. В исходных переменных: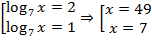. Подстановка  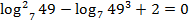– верное тождество,  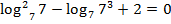– верное тождество.
Ответ: 7;49.

Простейшее логарифмическое неравенство имеет вид:
1) 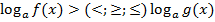. Здесь нужно рассматривать два случая – аналогично показательным неравенствам. Если основание логарифма больше единицы – логарифмическому неравенству ставится в соответствие простейшее неравенство вида f(x)>(<;≥;≤)g(x), причем знак исходного неравенства сохраняется. Если основание логарифма меньше единицы, то получаем неравенство f(x)<(>;≤;≥)g(x), т.е. знак исходного неравенства меняется на противоположный.
Частью решения неравенства является запись ОДЗ логарифмов, которые в него входят.
2) loga f(x)>(<;≥;≤) b. Оно решается по определению логарифма с проверкой знака неравенства по аналогии с предыдущим пунктом.
Как и в предыдущем случае частью решения неравенства является запись ОДЗ логарифмов.

Логарифмическое неравенство любой сложности нужно преобразовать до простейшего. Основные типы и методы преобразования логарифмических неравенств аналогичны логарифмическим уравнениям.
Пример: Решить неравенство .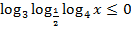
Решение: Выпишем ОДЗ логарифмов .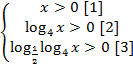

Перейдем к решению

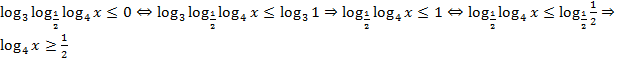
(автоматически выполнено ОДЗ [2]) 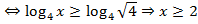 (автоматически выполнено ОДЗ [1]).
Осталось решить неравенство из ОДЗ [3] и проверить влияет ли оно на решение. .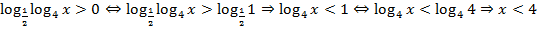
Объединяем решение ОДЗ с первичным решением неравенства 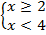. Как видим, ОДЗ повлияло на итоговое решение.
Ответ: x∈ [2;4).