Краткий конспект подготовки к ЗНО по математике №4-5 "Дробно-рациональные выражения. Формулы сокращенного умножения."

Урок 4-5. Дробно-рациональные выражения. Формулы сокращенного умножения

Формулы сокращенного умножения

Очень часто при разложении многочленов на множители применяются формулы сокращенного умножения. Вот наиболее важные из них:

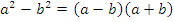
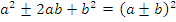
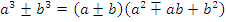
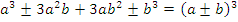
Сокращение рациональных дробей

Дробь, в числителе и знаменателе которой стоят многочлены, называется рациональной.
Чтобы сократить рациональную дробь, нужно ее числитель и знаменатель разложить на множители. При сокращении следует учитывать, что на ноль делить нельзя, поэтому нужно накладывать ограничения на значения переменных.
ОДЗ – область допустимых значений – это все те значения, которые могут принимать переменные, входящие в выражение, и при которых данное выражение имеет смысл.
Пример: сократить дробь

.

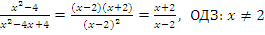
Действия с рациональными дробями

Все действия с рациональными дробями выполняются аналогично обыкновенным дробям, т.е. рациональные дроби точно так же можно складывать, вычитать, умножать, делить и возводить в степень.
Для сложения/вычитания рациональных дробей их нужно привести к общему знаменателю – для этого знаменатели исходных дробей нужно разложить на множители.
Пример: вычесть дроби

.
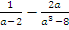Решение: 

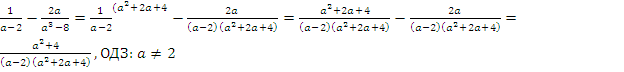
Ответ:

 .
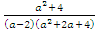Умножать и делить можно любые рациональные дроби, правила такие же, как для обыкновенных дробей: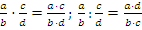 

при этом вместо  могут стоять любые многочлены. После того, как дроби записаны под общей дробной чертой, все многочлены нужно разложить на множители и максимально сократить.

Чтобы возвести рациональную дробь в степень, нужно возвести в степень и ее числитель, и знаменатель.
Пример:

.
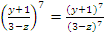Тождественные преобразования с дробями
Пример: упростить .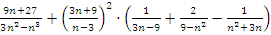
Решение:
1) Нужно привести дроби в скобках к общему знаменателю и выполнить действия. Числитель и знаменатель второй дроби домножим на (-1), чтобы все множители знаменателей стали однотипными: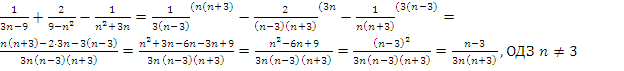

2) Выполним умножение:

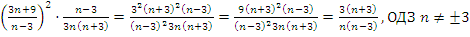
3) Выполним сложение. Для этого приведем дроби к общему знаменателю:

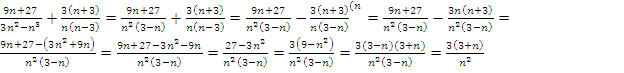
Ответ: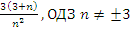 

Пример: упростить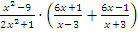

Решение:
1) Выполним сложение в скобках, для этого приведем дроби к общему знаменателю: 

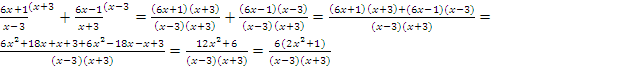
2) Умножим дроби:

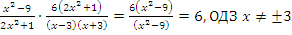
Ответ: .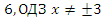

Доказательство тождеств

Пример: доказать тождество

.
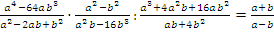Доказательство: разложим все многочлены в левой части на множители: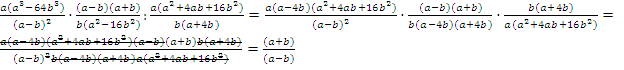

Тождество доказано.

 Тесты подготовки к ЗНО:

Онлайн-тест подготовки к ЗНО по математике №4 "Дробные рациональные выражения. Формулы сокращённого умножения."

Онлайн-тест подготовки к ЗНО по математике №5 "Дробно-рациональные выражения. Формулы сокращённого умножения"