Краткий конспект подготовки к ЗНО по математике №19-20 "Показательные уравнения и неравенства"

Урок 19-20. Показательные уравнения и неравенства

Преобразование выражений со степенями (повторение, закрепление)

Пример: Упростить выражение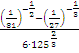 
Решение: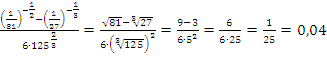 
Ответ: 0,04.

Методы решения показательных уравнений и неравенств

Простейшее показательное уравнение имеет вид: 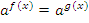, где a – действительное число, a>0.
В таком случае показательное уравнение заменяется более простым, чаще всего линейным или квадратным, вида: 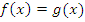. При решении показательных уравнений любой сложности цель – привести уравнение к виду  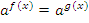и перейти к уравнению .

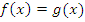Пример: Решить уравнение .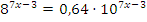
Решение: Обе части уравнения нужно поделить на :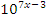
.
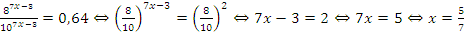Ответ: .
Некоторые показательные уравнения сводятся к квадратным.
Пример: Решить уравнение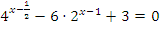 
Решение: .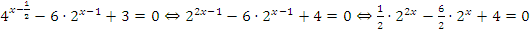

Удобно выполнить замену переменных : .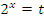
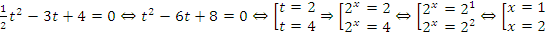Ответ: 1; 2.
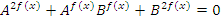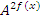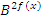Уравнения вида  называются однородными и решаются путем деления всего уравнения на одну из старших степеней  или . Далее вводится замена вида 
Пример: Решить уравнение .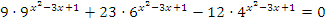
Решение: Нужно выполнить деление: 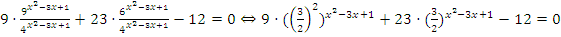. Теперь нужно ввести замену переменных: 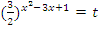, тогда: .
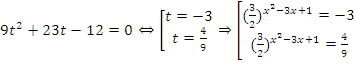Первое уравнение не имеет смысла, т.к. показательная функция не принимает отрицательных значений. Второе уравнение – простейшее показательное уравнение, от которого следует перейти к квадратному.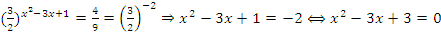
. У данного уравнения нет корней, т.к. его дискриминант отрицательный. Следовательно нет корней и у исходного уравнения.
Ответ: корней нет.

Простейшее показательное неравенство имеет вид: 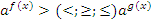, где a – действительное число, a>0.
Здесь нужно рассматривать два случая:
– когда основание степени a больше единицы, показательное неравенство заменяется более простым, чаще всего линейным или квадратным, вида: 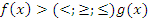, при чем сохраняется знак исходного неравенства;
– если же основание степени меньше единицы, то знак исходного неравенства следует поменять на противоположный.
При решении показательных неравенств любой сложности цель – привести неравенство к простейшему.
Основные типы показательных неравенств и методы их преобразования аналогичны показательным уравнениям.
Пример: Решить неравенство .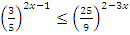
Решение: Приводим к одинаковому основанию 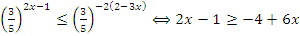, знак неравенства поменяли, т.к. 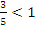. Далее решаем линейное неравенство и получаем .
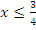Ответ: .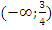

Системы показательных уравнений

Пример: Решить систему .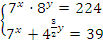
Решение: 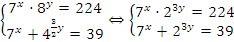. Нужно ввести замену переменных: 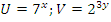, тогда: 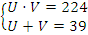. Такая система удобно решается методом подстановки, ее решение:  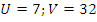и 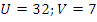. В исходных переменных:  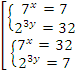– получена совокупность систем простейших показательных уравнений. Метод решения уравнений, которые входят в первую систему, нам уже известен, для решения второй нам понадобятся знания логарифмов, которые мы изучим в следующих темах.
Пример: .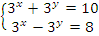
Решение: Здесь нужно применить такой прием: получить новую систему, первое уравнение которой это сумма исходных уравнений, а второе – разность. 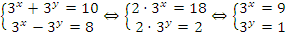– получена система простейших показательных уравнений, метод решения которых нам уже известен.