Краткий конспект подготовки к ЗНО по математике №12-13 Решение текстовых задач

Урок 12-13. Решение текстовых задач

Решение любой текстовой задачи состоит из трех этапов:
1) Анализ условия и обозначения величин.
2) Составление модели (уравнений).
3) Решение полученного уравнения (системы уравнений) и получение ответа на вопрос (вопросы) в условии.

Решение задач на пропорции

Решение таких задач основано на понятии пропорции и ее свойствах, которые рассмотрены ранее.
Пример: известно, что с одного гектара фермер собирает 3,5 тонны зерна. Какова площадь поля, если фермер собрал 27 тонн зерна?
Решение: нужно обозначить искомую величину за x и составить пропорцию:  .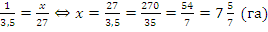
Ответ: .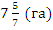

Решение задач на проценты

Выделяют три типа задач на проценты:
1) Найти, чему равен процент от числа.
2) Пусть задано число A и нужно найти x% от него. Решение: .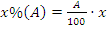
3) Найти, какой процент от числа составляет данное число.
Пусть заданы числа A и B, требуется определить, сколько процентов число B составляет от числа A. Решение: нужно обозначить искомый процент за x и составить пропорцию .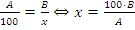
Найти число, зная, чему равен его процент.
Пусть задано число a, которое составляет x% от некоторого числа A, которое требуется найти. Решение: .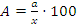
Пример: Первоначальная стоимость единицы продукции равнялась 75 грн. В течение первого года производства она повысилась на некоторое число процентов, а в течение второго года снизилась (по отношению к повышенной стоимости) на такое же число процентов, в результате чего она стала равна 72 грн. Определите проценты повышения и понижения стоимости единицы продукции.
Решение: нужно обозначить искомый процент за x, тогда в результате повышения цена составит: 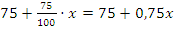. После понижения: .
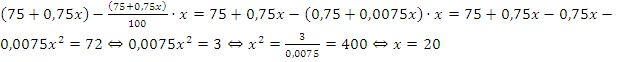Ответ: цена изменялась на 20%.

Решение задач на смеси, растворы и сплавы

Решение основывается на формуле: 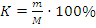, где K – процент вещества в растворе/смеси/сплаве; m – масса/объем вещества; M – масса/объем всей смеси/сплава/раствора. Принцип решения следующий:
1) Определить массу/объем всех смесей, о которых идет речь в задаче.
2) Определить массу/объем дополнительного вещества во всех смесях, о которых идет речь в задаче.
3) Определить процентное содержание дополнительного вещества во всех смесях, о которых идет речь в задаче.
4) Выбрать удобную величину и обозначить ее за x, а остальные величины выразить через x по формуле .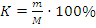
5) Получить ответ, решив уравнение или систему.
Пример: Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
Решение: для удобства можно составить таблицу:

	Объем раствора	Объем вещества	Процентное содержание
Раствор 1	4 л		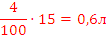15%
Раствор 2	6 л		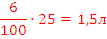25%
Раствор 3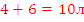

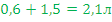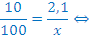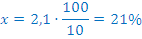В таблице красным обозначены первичные расчеты по данным условия; зеленым – расчеты по данным, полученным в результате первичных расчетов. После того, как все возможные данные вычислены, искомый процент обозначен за x, составлена пропорция и получен ответ (выделено синим цветом).
Ответ: 21%.

Решение задач на движение

Можно выделить несколько типов наиболее распространенных задач на движение:
1) Движение по воде;
2) Движение по окружности;
3) Движение по прямой.
Здесь важно знать формулу равномерного движения: 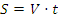, где S – пройденный путь, V – скорость, t – время движения.
Пример: Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
Решение: за два часа скорый поезд проехал 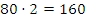 км, значит расстояние между поездами к этому моменту стало  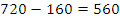км. С этого момента поезда сближаются со скоростью  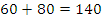км/ч. Найдем время, через которое они встретятся:  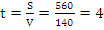часа.
Ответ: 4 ч.

Решение задач на работу

В задачах на совместную работу весь объем работы, как правило, принимается за единицу.
Продуктивность (производительность, скорость) труда – это объем работы, который может быть выполнен в единицу времени.
Решение основано на формуле: 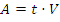, где A – весь объем работы, t – время, за которое выполнена вся работа, V – продуктивность труда.
Пример: Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Решение: объем работы нужно принять за единицу. Тогда производительность труда каждого рабочего составляет: 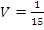. Пусть время совместной работы x, при этом несложно догадаться, что совместная продуктивность труда равна суммарной продуктивности двух рабочих.
Согласно формуле: 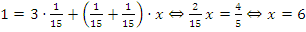 часов. Рабочие вместе работали 6 часов, кроме того первый работал еще три часа. Так, на выполнение заказа ушло 3+6=9 часов.
Ответ: 9 ч.