Краткий конспект подготовки к ЗНО по математике №30 "Функции"
Урок 30. Функции
Тригонометрические функции
1. Функция синус
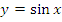 – график функции синусоида.
– график функции синусоида.
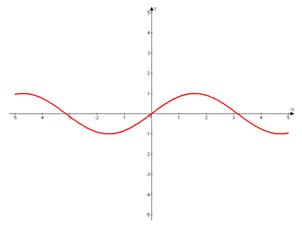
Свойства:
а) Область определения: 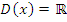 ;
;
б) Область значений: 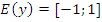 ;
;
в) Функция имеет период 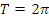 ;
;
г) Функция нечетная: 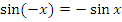 ;
;
д) На интервале 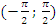 функция монотонно возрастает, на интервале
функция монотонно возрастает, на интервале 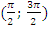 – монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
– монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция непрерывна.
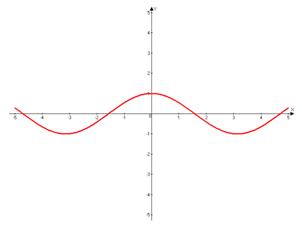
2. Функция косинус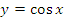 – график функции синусоида, сдвинутая на
– график функции синусоида, сдвинутая на 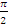 влево относительно оси ординат.
влево относительно оси ординат.
Свойства:
а) Область определения: 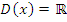 ;
;
б) Область значений: 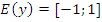 ;
;
в) Функция имеет период 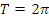 ;
;
г) Функция четная: 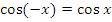 ;
;
д) На интервале 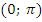 функция монотонно убывает, на интервале (
функция монотонно убывает, на интервале (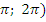 – монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
– монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция непрерывна.
3. Функция тангенс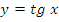
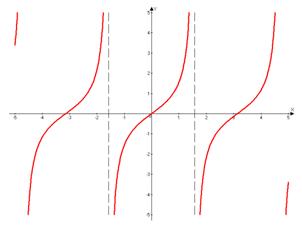
Свойства:
а) Область определения: 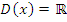 кроме
кроме 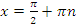 , где
, где 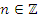 ;
;
б) Область значений: 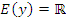 ;
;
в) Функция имеет период 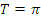 ;
;
г) Функция нечетная: 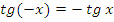 ;
;
д) На интервале 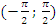 функция монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
функция монотонно возрастает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция имеет разрывы и вертикальные асимптоты 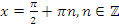 .
.
4. Функция котангенс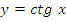
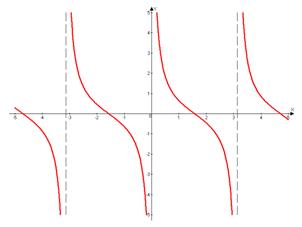
Свойства:
а) Область определения: 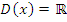 кроме
кроме 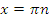 , где
, где 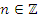 ;
;
б) Область значений: 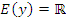 ;
;
в) Функция имеет период 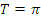 ;
;
г) Функция нечетная: 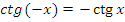 ;
;
д) На интервале 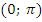 функция монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
функция монотонно убывает и так далее с учетом периодичности. На всей области определения функция не монотонна;
е) Функция имеет разрывы и вертикальные асимптоты 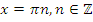 .
.
Обратные тригонометрические функции
1. Функция арксинус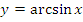
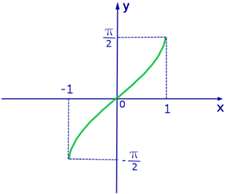
Свойства:
а) Область определения: 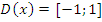 ;
;
б) Область значений: 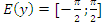 ;
;
в) Функция не периодичная;
г) Функция нечетная: 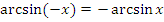 ;
;
д) Функция монотонно возрастает на всей области определения;
е) Функция непрерывна.
2. Функция арккосинус
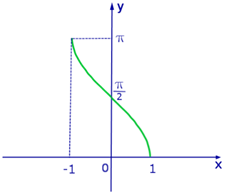
Свойства:
а) Область определения: 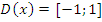 ;
;
б) Область значений: 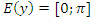 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения;
е) Функция непрерывна.
3. Функция арктангенс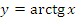
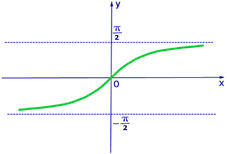
Свойства:
а) Область определения: 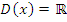 ;
;
б) Область значений: 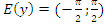 ;
;
в) Функция не периодичная;
г) Функция нечетная: 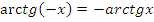 ;
;
д) Функция монотонно возрастает на всей области определения;
е) Функция непрерывна.
4. Функция арккотангенс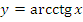
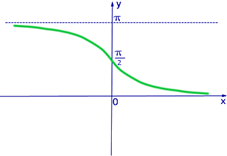
Свойства:
а) Область определения: 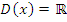 ;
;
б) Область значений: 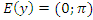 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения;
е) Функция непрерывна.
Показательная функция
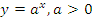
В данном случае необходимо рассматривать два случая.
1. Основание степени больше единицы: 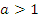 .
.
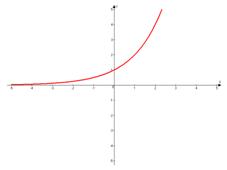
Свойства:
а) Область определения: 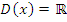 ;
;
б) Область значений: 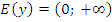 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно возрастает на всей области определения и имеет горизонтальную асимптоту 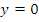 ;
;
е) Функция непрерывна.
2. Основание степени меньше единицы: 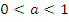 .
.
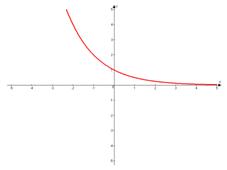
Свойства:
а) Область определения: 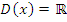 ;
;
б) Область значений: 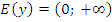 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения и имеет горизонтальную асимптоту 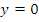 ;
;
е) Функция непрерывна.
Логарифмическая функция
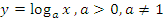
Здесь также необходимо рассматривать два случая.
1. Основание логарифма больше единицы: 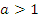 .
.
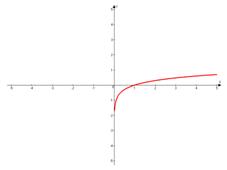
Свойства:
а) Область определения: 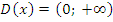 ;
;
б) Область значений: 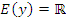 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно возрастает на всей области определения и имеет вертикальную асимптоту 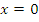 ;
;
е) Функция непрерывна.
2. Основание логарифма меньше единицы: 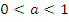 .
.
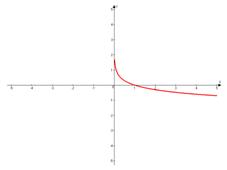
Свойства:
а) Область определения: 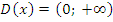 ;
;
б) Область значений: 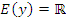 ;
;
в) Функция не периодичная;
г) Функция общего вида;
д) Функция монотонно убывает на всей области определения и имеет вертикальную асимптоту 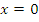 ;
;
е) Функция непрерывна.
Преобразование графиков функций
Выше были представлены графики некоторых простейших функций. Также ранее мы уже изучали графики линейной, квадратичной и др. функций (см. конспект №10). Графики большинства более сложных функций можно получить, преобразовывая известные графики простейших функций.
Рассмотрим ряд правил преобразования графиков функций.
| Преобразование | Пример |
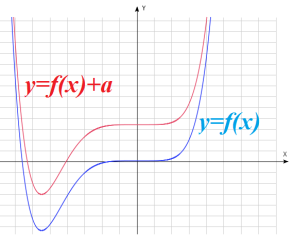
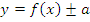 : график получается путем сдвига графика функции : график получается путем сдвига графика функции 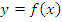 на a единиц вверх (при «+») или вниз (при «-») на a единиц вверх (при «+») или вниз (при «-») |
|
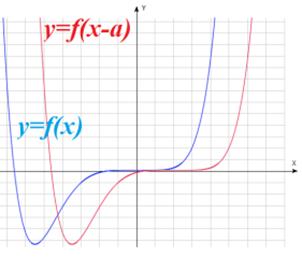
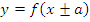 : график получается путем сдвига графика функции : график получается путем сдвига графика функции 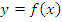 на a единиц влево (при «+») или вправо (при «-») на a единиц влево (при «+») или вправо (при «-») |
|
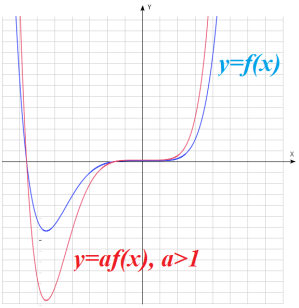
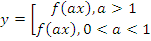 : график получается путем сжатия ( : график получается путем сжатия (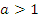 ) или растяжения ( ) или растяжения (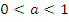 ) графика функции ) графика функции 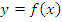 в a раз относительно оси ординат в a раз относительно оси ординат |
|
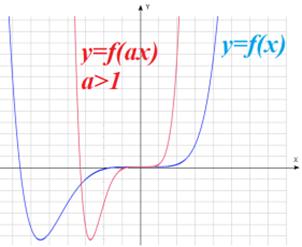
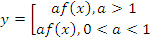 : график получается путем растяжения ( : график получается путем растяжения (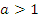 ) или сжатия ( ) или сжатия (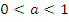 ) графика функции ) графика функции 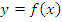 в a раз относительно оси абсцисс в a раз относительно оси абсцисс |
|
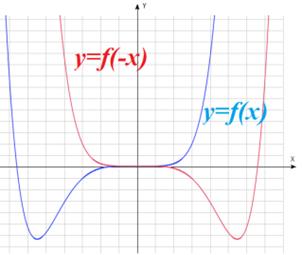
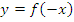 : график получается путем симметричного отображения графика функции : график получается путем симметричного отображения графика функции 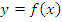 относительно оси ординат относительно оси ординат |
|
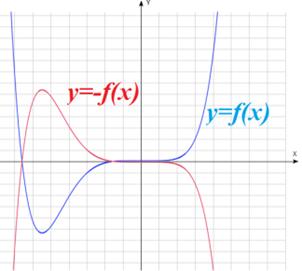
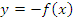 : график получается путем симметричного отображения графика функции : график получается путем симметричного отображения графика функции 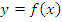 относительно оси абсцисс относительно оси абсцисс |
|
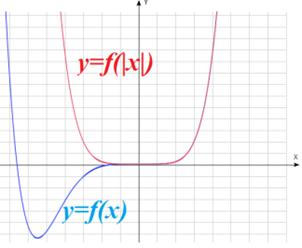
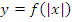 : график получается путем добавления симметричного отображения части графика функции : график получается путем добавления симметричного отображения части графика функции 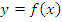 , которая построена при , которая построена при 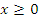 , относительно оси ординат и отбрасывания части графика функции, которая построена при , относительно оси ординат и отбрасывания части графика функции, которая построена при 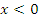 |
|
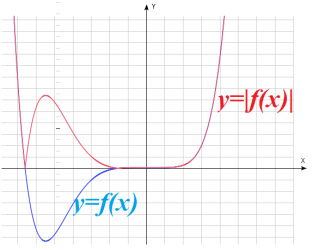
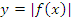 : график получается путем симметричного отображения отрицательной части графика функции : график получается путем симметричного отображения отрицательной части графика функции 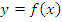 относительно оси абсцисс, при этом положительная часть графика остается без изменений относительно оси абсцисс, при этом положительная часть графика остается без изменений |
|