Краткий конспект подготовки к ЗНО по математике №11 Уравнения с модулями. Системы уравнений

Урок 11. Уравнения с модулями. Системы уравнений

Решение уравнений, содержащих неизвестную под модулем

Уравнения, в которых переменная стоит под знаком модуля и такой модуль один, в простейшем случае сводятся к уравнениям вида , где a – действительное число. Если , то решений нет, если , то решение подобного уравнения:

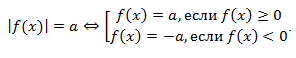
Пример: .
Решение:

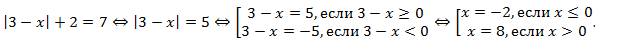
Ответ: -2;8.
Также уравнение с одним модулем может иметь вид . Решение такого уравнения аналогично.
Пример: 
Решение:

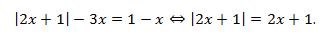
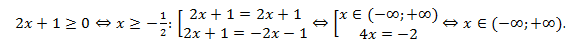
Объединив решение с ограничением на правую часть уравнения, получаем

 
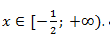
Ответ: .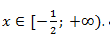
При решении уравнений с несколькими модулями вида нужно придерживаться алгоритма:
Определить нули подмодульных выражений, решив уравнения:  и т.д.;
Разбить множество значений аргумента на интервалы определенными в п.1 нулями;
Определить знаки подмодульных выражений на каждом интервале;
Рассмотреть решение уравнения на каждом интервале отдельно, раскрыв модули с учетом знаков подмодульных выражений.
Пример: .
Решение: 1. Определяем нули: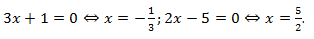  
2. Множество значений аргумента разбито на интервалы: .
3. Определяем знаки подмодульных выражений:

4. Рассмотрим решение уравнения для трех случаев.

При : 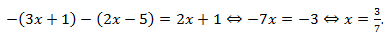. Найденный корень не входит в рассматриваемый интервал.
При :  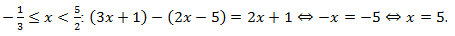Найденный корень не входит в рассматриваемый интервал.
При : 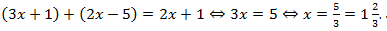. Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.
Ответ: корней нет.

Системы линейных уравнений

Система вида 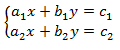 называется системой линейных уравнений с двумя переменными, здесь  – действительные числа. Решить систему означает найти все пары значений , которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.
1. Метод подстановки.

Заключается в том, что в одном из уравнений системы нужно выразить одну переменную через другую и подставить полученное выражение во второе уравнение системы.
Пример: 

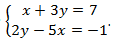
Решение:

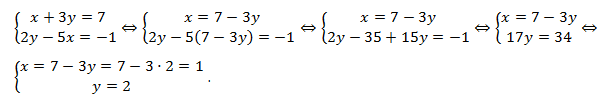
Ответ: (1;2).
2. Метод алгебраического сложения.

Заключается в том, что нужно получить противоположные коэффициенты при одной из переменных уравнения и сложить уравнения, при этом избавившись от одной переменной. Таким образом, решение системы сводится к решению линейного уравнения с одной переменной.
Пример: 

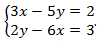
Решение: 

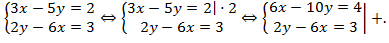
Получаем 

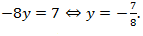
Ответ: .
3. Графический метод.

Заключается в построении графиков двух линейных функций. Если прямые пересеклись – координаты точки пересечения будут единственным решением системы. Если прямые параллельны или совпали, то система не имеет решений или, соответственно, имеет бесконечно много решений.

Количество решений системы линейных уравнений

Система двух линейных уравнений с графической точки зрения представляет собой две прямые, построенные в системе координат. Две прямые могут пересекаться только в одной точке. Также они могут совпадать или быть параллельными. Очевидно, что система двух линейных уравнений имеет только три варианта решения:
Единственное решение (прямые пересекаются);
Нет решений (прямые параллельны);
Бесконечно много решений (прямые совпали).
Для системы 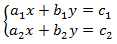 существует простой способ определить наличие решений:
– если  , то система имеет бесконечное количество решений;
– если  , то система не имеет решений;
– если  , то система имеет одно решение.
Системы уравнений высших степеней
Системы, в которых одно из уравнений линейное, как правило, решаются методом подстановки. Если в системе оба уравнения нелинейные, то применяют также комбинирование уравнений с целью получения нового уравнения, которое можно разложить на простые множители.
Пример: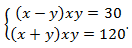 
Решение: Нужно раскрыть скобки: 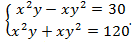 Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания:  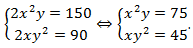Нужно умножить уравнения системы:  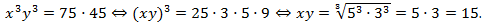Теперь можно применить способ подстановки: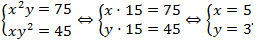 
Ответ: 5;3.