Краткий конспект подготовки к ЗНО по математике №29 Функции

Урок 29. Функции

Понятие функциональной зависимости

Функциональная зависимость устанавливает правило, согласно которому по значению независимой переменной – аргумента, можно найти значение зависимой переменной – функции. Слово функция употребляют в двух значениях: это и сама функциональная зависимость, и зависимая переменная.
Самое главное требование к функциональной зависимости: единственность от аргумента к функции. Это означает, что каждому значению аргумента может соответствовать единственное значение функции, в то время как одному значению функции может соответствовать сколь угодно много значений аргумента.
Функция - это закон соответствия между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует только одно определенное значение другой величины y (функции или зависимой переменной).
Основные способы задания числовых функций:
1. Аналитический способ – задание функции с помощью формулы.
Обозначать в общем виде такую формулу принято обычно как 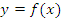, где под x понимают аргумент, а под y значение функции.
2. Табличный способ – задание функции с помощью таблицы связанных друг с другом значений.
3. Графический способ – задание функции с помощью изображения точек в системе координат, когда одной координате точек поставлена в однозначное соответствие другая ее координата.

Область определения и область значений

Область определения функции – это множество значений аргумента, для которых функция имеет смысл. Иными словами, это допустимые значения икса. Это множество принято обозначать D или D(x).
Если функция задана аналитически, как это чаще всего бывает, то в таком случае удобнее всего сначала найти те значения аргумента, при которых функция не имеет смысла, и исключить их из множества действительных чисел.
Основные случаи, в которых необходимо искать не имеющие смысла для функции аргументы:
1. Наличие в функции деления на выражение, содержащее неизвестную. В таком случае исключаются те аргументы, при которых возникает деление на ноль.
2. Присутствие в функции корня четной степени из выражения, содержащего неизвестную. При этом необходимо исключить аргументы, при которых подкоренное выражение отрицательно, в таком случае удобно сразу накладывать условие, что подкоренное выражение больше или равно нулю.
3. Наличие в функции логарифмов, содержащих неизвестные выражения. В общем виде это можно записать так: если функция содержит 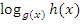, где g(x) и h(x) - это выражения, содержащие неизвестную, то областью определения будет решение системы неравенств
.
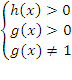Область значений функции – это множество значений функции, которые она принимает в своей области определения. Т.е. в стандартной записи функции это значения ее игрека. Множество значений функции принято обозначать E или E(y).
Задания на поиск области значений функции в ВНО встречаются достаточно редко.

Понятия четности и монотонности

Функция называется четной, если для всех значений аргумента верно следующее –при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так .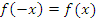
График такой функции симметричен относительно оси 0y.
Пример: 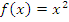.  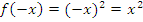– функция четная.
Функция называется нечетной, если для всех значений аргумента верно следующее – при изменении знака аргумента, она меняет свое значение на противоположное. Формульная запись этого выглядит так .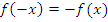
График такой функции симметричен относительно начала координат.
Пример: 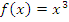.  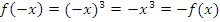– функция нечетная.
Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида. У таких функций нет симметрии относительно оси 0y и начала координат.
Важным свойством функции является ее монотонность. Выделяют следующие виды монотонности функций:
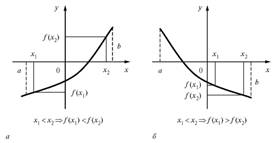
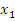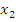1. Функция f(x) возрастает, если на некотором интервале, если для любых двух точек  и  этого интервала таких, что  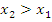выполнено, что 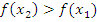. Т.е. большему значению аргумента соответствует большее значение функции;
2. Функция f(x) убывает, если на некотором интервале, если для любых двух точек 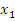 и 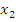 этого интервала таких, что  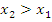выполнено, что 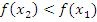. Т.е. большему значению аргумента соответствует меньшее значение функции;

3. Функция f(x) неубывает, если на некотором интервале, если для любых двух точек 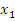 и 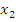 этого интервала таких, что  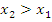выполнено, что ;

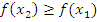4. Функция f(x) невозрастает, если на некотором интервале, если для любых двух точек 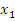 и 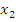 этого интервала таких, что  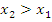выполнено, что .

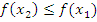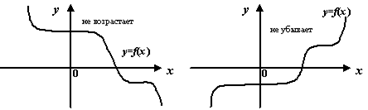
Для первых двух случаев еще применяют термин «строгая монотонность».
Два последних случая являются специфическими и задаются обычно в виде композиции из нескольких функций.
Пример: Функция 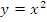 монотонно убывает при  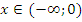и монотонно возрастает при .

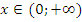Обратные функции

Если функция 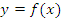 достигает каждого своего значения в единственной точке ее области определения, то можно задать функцию 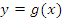, которая называется обратной к функции 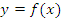. Причем, для каждого a из области определения f, если 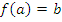, то 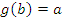. Функции f и g называются взаимнообратными.
График обратной функции симметричен графику прямой функции относительно прямой .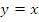

Периодические функции

Функция 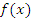 называется периодической с периодом 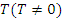, если для любого x верно: если функция определена в одной из точек x или 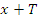, то она определена и во второй точке, а значения функции в обеих точках равны, то есть .
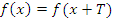Число T называется периодом функции.
Все тригонометрические функции являются периодическими.

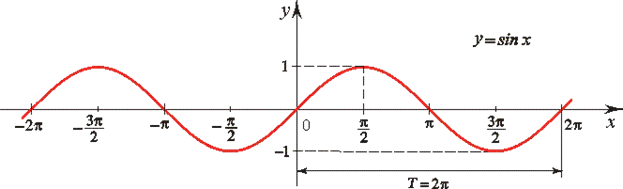
Понятие ГМТ

Графическое изображение однозначной функции называют построением графика функции, а изображение многозначной функции – построением геометрического места точек или ГМТ.
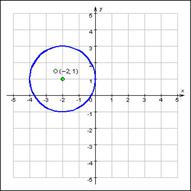
Пример: Графическое изображение уравнения 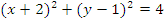 будет ГМТ, а конкретно изображением окружности: