Краткий конспект подготовки к ЗНО по математике №17-18 "Иррациональные уравнения и неравенства"

Урок 17-18. Иррациональные уравнения и неравенства

Решение иррациональных уравнений

Иррациональными называются такие уравнения, в которых переменная стоит под знаком корня.
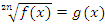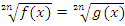1) Уравнения вида  или  решаются путем возведения обеих частей в степень корня. Здесь обязательна проверка полученных корней, так как под корнем четной степени может стоять только положительное число или ноль и сам корень может принимать только неотрицательные значения.
2) Уравнения вида 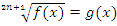 или 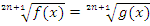 решаются путем возведения обеих частей в степень корня. Здесь проверка не нужна, так как под корнем может стоять любое действительное число и сам корень принимает любые значения.
Пример: Решить уравнение .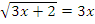
Решение: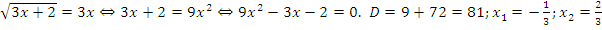  
Проверка: 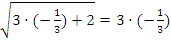. Квадратный корень принимает отрицательное значение, что невозможно – данный корень лишний. 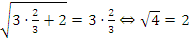, т.е. корень  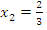подходит.
Ответ: 2/3.

Решение иррациональных неравенств

Иррациональными называются такие неравенства, в которых переменная стоит под знаком корня.

1) Неравенство вида 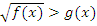. При решении необходимо рассмотреть два случая:
а) если правая сторона неравенства неотрицательна, то мы имеем выражение вида «неотрицательное число»>«неотрицательное число», что выполнено не всегда и его необходимо полноценно решать

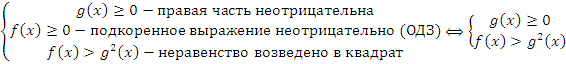
Стоит обратить внимание, что второе условие выполнено автоматически, если выполнено третье, т.е. его можно не записывать при решении.
б) или если правая сторона неравенства отрицательна, то имеем выражение вида «неотрицательное число»>«отрицательное число», что выполнено всегда с учетом ОДЗ, т.е. 

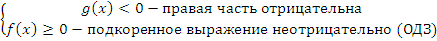
Множества из решений обоих случаев объединяют и получают ответ.
Пример: Решить неравенство .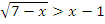
Решение: 

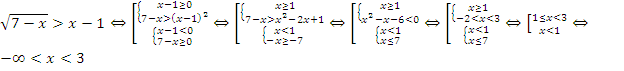
Ответ: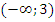 

2) Неравенство вида 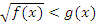. При решении достаточно рассмотреть одну эквивалентную систему неравенств: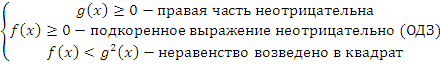

В отличие от предыдущего варианта случай 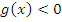 не имеет смысла, так как тогда мы получаем выражение вида «неотрицательное выражение»<«отрицательное выражение», что невозможно.

3) Неравенства вида 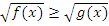 заменяются эквивалентной системой: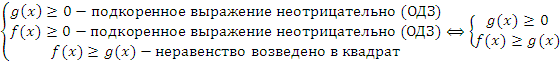

Второе условие выполнено автоматически при выполнении третьего, поэтому его можно не писать.

4) Неравенства вида 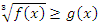 заменяются эквивалентным неравенством:
.
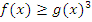В них не записываются ограничения на ОДЗ, т.к. подкоренное выражение в корне нечетной степени и сам корень может принимать любые значения.

Замечание. Иррациональные неравенства можно решать графическим методом.
Пример: Решить неравенство графически: .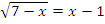
Решение: Первая функция монотонно убывает, вторая монотонно возрастает на области определения.

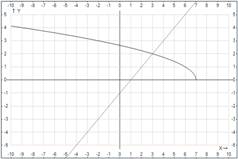
Если уравнение 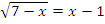 имеет корень, то он единственный, по графику легко его увидеть: 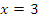. Эта точка отвечает пересечению, т.е. равенству двух функций.
Далее по графику выписываем множество аргументов, при которых выполнено неравенство.
Конечно же, такой способ решения эффективен в том случае, когда точки пересечения функций являются целыми и небольшими числами.
Ответ: .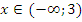

Неравенства других четных и нечетных степеней решаются аналогично.