Краткий конспект подготовки к ЗНО по математике №1 "Основы арифметических знаний."

Подготовка к ВНО. Математика.

Конспект 1. Основы арифметических знаний.

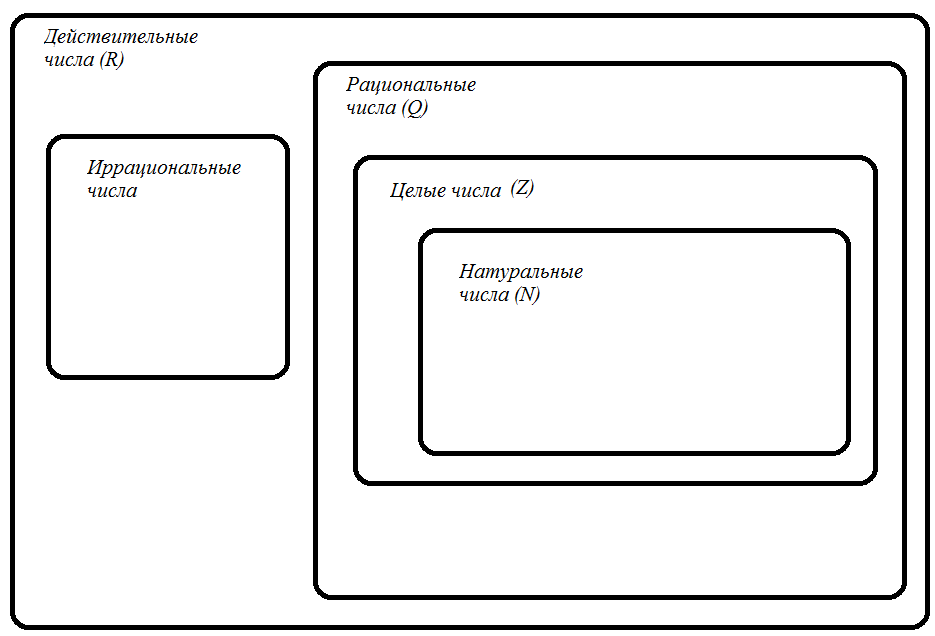
Числовые множества

Все числа, которые используются в математике, принадлежат определённым числовым множествам.

Натуральные числа (N) – это числа, используемые при счёте. Наименьшим числом является 1. Пример: 1, 2, 3, 100 и т. д.

Целые числа (Z) – натуральные числа, им противоположные и 0. Пример: -2, -1, 0, 1, 2 и т. д.

Рациональные числа (Q) – числа, которые можно представить в виде дроби , где m - целое число, n - натуральное число. Вдобавок, заметим, что бесконечные периодические дроби принадлежат к множеству рациональных чисел. Пример: .

Иррациональные числа – числа, в записи которых присутствует бесконечная непериодическая дробь. Пример: .

Действительные числа (R) – множество, образованное двумя подмножествами – рациональных и иррациональных чисел.

Для того, чтобы сразу определить, на какие числа делится заданное число, в математике используют признаки делимости. Самыми популярными являются следующие признаки делимости.

1. 1.  Признак делимости на 2.
2.  Число делится на 2, если последняя цифра числа является 0, 2, 4, 6, 8. Пример: 2014 делится на 2, так как последняя цифра – 4.
3. 2. Признак делимости на 3.

Число делится на 3, если сумма цифр числа делится на 3. Пример: 22143 делится на 3, так как сумма его цифр равна 2+2+1+4+3 = 12, что делится на 3.

1.  3. Признак делимости на 4.

Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Пример: 61348 делится на 4, так как число 48 делится на 4.

1.  4. Признак делимости на 5.

Число делится на 5, если последняя цифра числа  - 0 или 5. Пример: 3200 делится на 5, так как последняя цифра - 0. Число 9875 делится на 5, так как последняя цифра - 5.

1. 5.  Признак делимости на 9.

Число делится на 9, если сумма цифр числа делится на 9. Пример: 72243 делится на 3, так как сумма его цифр равна 7+2+2+4+3 = 18, что делится на 9.

1. 6.  Признак делимости на 10.

Число делится на 10, если последняя цифра числа  - 0. Пример: 37520 делится на 10, так как последняя цифра - 0. 

Работа с дробями

Дробь - число, состоящее из одной или нескольких частей (долей) единицы. Дробь можно представить в виде , где m – числитель, n – знаменатель. В случае, если знаменатель дроби равен 10, 100, 1000 и т. д., дробь называется десятичной и записывается в виде 0,1; 0,01; 0,001 соответственно.
В математике существует негласное разделение дробей на две группы.
1) Дроби с одинаковыми знаменателями. Для того, чтобы сравнить две дроби с одинаковыми знаменателями, необходимо сравнить их числители. Та дробь больше, у которой числитель больше.
2) Дроби с разными знаменателями. Для того, чтобы сравнить две дроби с разными знаменателями, необходимо привести их к общему знаменателю, а затем сравнить две дроби с одинаковыми знаменателями.
Чтобы привести дроби к общему знаменателю, необходимо воспользоваться основным свойством дроби – числитель и знаменатель любой дроби можно одновременно умножить и разделить на одно и то же число.
Пример: Привести дроби  и  к общему знаменателю. Выполним умножение числителя и знаменателя первой дроби на 7, а второй – на 4.

.
Сложение и вычитание дробей выполняется по такому правилу: в случае сложения/вычитания дробей с одинаковыми знаменателями, выполнить сложение/вычитание числителей, а знаменатель оставить прежним. Если складываются две дроби с разными знаменателями, необходимо привести их к общему знаменателю, а потом выполнить действие дробей с одинаковыми знаменателями.
Пример: .
Умножение дробей выполняется по такому правилу: числители и знаменатели дробей попарно перемножаются.
Пример: .
Деление дробей выполняется по такому правилу: дробь-делитель необходимо «перевернуть», затем выполнить умножение.
Пример: .

Online-тест подготовки к ЗНО по математике №1 "Основы арифметических знаний"