Краткий конспект подготовки к ЗНО по математике №2 "Отношения и пропорции. Десятичные дроби"

Урок 2. Отношения и пропорции. Десятичные дроби.

Понятия отношения и пропорции

Отношением двух чисел называется их частное. Пример:  и т.д. Отношение двух чисел показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Пропорцией называется равенство двух отношений. Пример: . Это читается: a относится к b так же как c относится к d. Величины a и d стоят «по краям» пропорции – они называются крайними, величины b и c в свою очередь называются средними.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов:

Из основного свойства вытекает: чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов пропорции разделить на известный крайний член. Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов пропорции разделить на известный средний член.
Пример: толщина 300 листов бумаги для принтера составляет 3,3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?
Решение: пусть x см — толщина пачки бумаги из 500 листов. Логика составления пропорции: пачке из 300 листов соответствует толщина в 3,3см, тогда пачке из 500 листов соответствует толщина в x см:

По основному свойству пропорции:

Ответ: пачка из 500 листов имеет толщину 5,5 см.

Понятие десятичной дроби. Операции над десятичными дробями

Десятичной дробью называют обыкновенную дробь, знаменатель которой кратен десяти (т.е. 10, 100, 1000 и т.д.), дробная часть записывается через запятую после целой части. Пример:  и т.д.
Арифметические операции над конечными непериодическими десятичными дробями выполняются аналогично тем же операциям с целыми числами – «в столбик»:
1. Сложение и вычитание. Важно подписывать разряд под разрядом как в целой части, так и в дробной. Если десятичных разрядов не хватает (как в числах 9,18 и 3,13 в дальнейшем примере), они заменяются нолями, эти нули не пишут при письменном выполнении действий.
Пример:

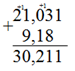 или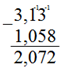 

Умножение. При записи чисел запятые не учитываются, записывается последняя цифра под последней, не зависимо от разрядов. Далее выполняется обыкновенное умножение «в столбик», в результате отделяется дробная часть – она составляет столько знаков, сколько суммарно содержат множители.
Пример: вычислить 7,05•5,4.
Решение: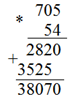 

В результате нужно отделить три десятичных знака, т.к. у первого множителя два знака после запятой, у второго один – в сумме три.
Ответ: 7,05•5,4=38,070=38,07.
3. Деление. Перед тем, как делить десятичные дроби, делимое и делитель нужно домножить на такое одинаковое число (10, 100, 1000 и т.д.), чтобы оба они стали целыми числами.
Пример: вычислить 48,18:0,3.
Решение: Нужно оба числа умножить на 100: 48,18:0,3=4818:30.

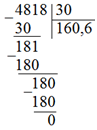
Ответ:160,6

Сравнение десятичных дробей можно выполнить двумя способами: сравнить соответствующие заданным дробям обыкновенные дроби или выполнить поразрядное сравнение. Поразрядное сравнение десятичных дробей аналогично сравнению натуральных чисел. Сравнение значений разрядов выполняется от старшего разряда к младшему. Та дробь, в старшем сравниваемом разряде которой стоит большее число, будет больше.
Пример: Сравнить 4,18 и 4,187.
Решение: Целая часть одинакова, первые два разряда дробной части одинаковы, нужно сравнить третий разряд. У первой дроби он равен нулю, у второй семи. 7>0⇒4,187>4,18.
Ответ: 4,187>4,18.

Связь между обыкновенными и десятичными дробями.

Чтобы перевести обыкновенную дробь в десятичную, нужно выполнить деление в столбик – в случае если знаменатель дроби не кратен десяти и при разложении на простые множители содержит любые числа кроме 2 и 5.
Если же знаменатель является степенью 10 или может стать таковым при домножении числителя и знаменателя дроби на некоторое число, то перевод осуществляется проще: запятая в числителе обыкновенной дроби перемещается влево на столько порядков, сколько нулей в знаменателе.
Примеры:
1. …

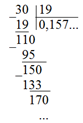
2.  и т.д.
3.
Чтобы перевести десятичную дробь в обыкновенную, нужно ее дробную часть записать в виде обыкновенной дроби со знаменателем 10, 100, 1000 и т.д. и сократить (если возможно).
Пример:

Периодические десятичные дроби

Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же последовательности, называется периодической десятичной дробью. При этом повторяющуюся последовательность цифр принято записывать в скобках.
Пример: 3,03030303…=3,(03);1,666…=1,(6);2,015333…=2,015(3)

Округление

Десятичную дробь можно округлить как до целого числа, так и до любого дробного разряда.
Алгоритм округления: подчеркнуть цифру округляемого разряда; если справа от подчёркнутой цифры стоит цифра 0, 1, 2, 3 или 4, то подчёркнутую цифру оставить без изменений, а все цифры справа от нее отбросить. Если справа от подчёркнутой цифры стоит цифра 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличить на единицу, а все цифры справа от нее отбросить.
Пример: округлить до сотых 3,1542 и 0,0192.
Решение: 3,1542=3,15 (в сотых стоит цифра пять, справа от нее цифра 4 – пятерка остается без изменений, четверка и двойка отбрасываются).
0,0192=0,02 (в сотых стоит цифра 1, справа от нее цифра 9 – единица увеличивается на один – превращается в двойку, девятка и двойка отбрасываются).

 Тесты подготовки к ЗНО:
Онлайн-тест подготовки к ЗНО по математике №2 "Отношения и пропорции. Десятичные дроби"