Онлайн-урок №15 "Функции"
Онлайн-урок №15 "Функции"
4.02.2016 в 18.30
Конспекты к уроку:
Система координат xOy
Для того, чтобы прямая стала координатной осью, она должна иметь направление, точку начала отсчета и масштаб.
Прямоугольная (или декартова) система координат на плоскости задается парой взаимно перпендикулярных координатных осей: oX, направленной слева направо и oY, направленной снизу вверх, имеющих общее начало в точке O, и одинаковый масштаб.
Горизонтальная ось x называется осью абсцисс и имеет уравнение  . Вертикальная ось y называется осью ординат и имеет уравнение
. Вертикальная ось y называется осью ординат и имеет уравнение  .
.
Любой график функции, проходящий через точку с координатой  , где a – произвольное действительное число, пересекает ось абсцисс. Любой график функции, проходящий через точку с координатой
, где a – произвольное действительное число, пересекает ось абсцисс. Любой график функции, проходящий через точку с координатой  , где b – произвольное действительное число, пересекает ось ординат.
, где b – произвольное действительное число, пересекает ось ординат.
Наиболее распространенные функции, их графики и свойства
1)  – вертикальная и горизонтальная прямые соответственно.
– вертикальная и горизонтальная прямые соответственно.
Пример:  .
.
2)  – линейная функция (график – прямая линия).
– линейная функция (график – прямая линия).
Метод построения: «по точкам» – необходимо подставить вместо аргумента любые два числовые значения и вычислить какие при этом получаются значения функции. Для удобства полученные данные вносят в специальную табличку. Для построения прямой достаточно провести ее через две точки, нанесенные в системе координат.
Пример: 
Решение: подставим в функцию произвольные значения аргумента

Занесем значения в табличку:
| x | y |
| 0 | -1 |
| 1 | 1 |
Нанесем точки в системе координат и проведем через них график прямой: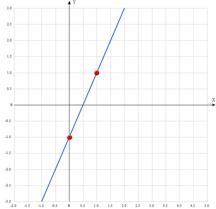
В зависимости от знаков коэффициентов можно определить, как проходит график линейной функции:
А.  : угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в положительном луче;
: угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в положительном луче;
Б.  : угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в положительном луче;
: угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в положительном луче;
В.  : угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в отрицательном луче;
: угол между прямой и положительным направлением оси абсцисс острый, пересекает ось ординат в отрицательном луче;
Г.  : угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в отрицательном луче.
: угол между прямой и положительным направлением оси абсцисс тупой, пересекает ось ординат в отрицательном луче.
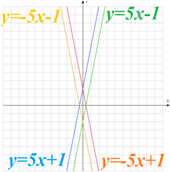
Вывод: коэффициент k отвечает за угол между положительным направлением оси абсцисс и прямой; коэффициент b отвечает за точку пересечения с осью ординат.
3)  – квадратичная функция (график – парабола).
– квадратичная функция (график – парабола).
Метод построения: «по вершине» (самый удобный) – необходимо вычислить координаты вершины параболы, а затем построить ее ветви с учетом их направления и пересечения осей координат.
Координаты вершины: 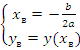
В зависимости от знаков коэффициентов можно охарактеризовать график, не выполняя построения.
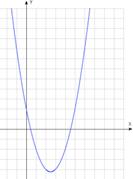
Коэффициент a отвечает за направление ветвей параболы. При  ветви направлены вверх, при
ветви направлены вверх, при  вниз.
вниз.
Коэффициент c отвечает за точку пересечения с осью ординат: при  парабола пересекает ось ординат в положительном луче; при
парабола пересекает ось ординат в положительном луче; при  проходит через начало координат; при
проходит через начало координат; при  – пересекает ось в отрицательном луче.
– пересекает ось в отрицательном луче.
Коэффициент b при определенном коэффициенте a задает положение вершины по оси абсцисс:
А. При  , вершина расположена в левой полуплоскости;
, вершина расположена в левой полуплоскости;
Б. При  , вершина расположена в правой полуплоскости;
, вершина расположена в правой полуплоскости;
В. При  , вершина расположена в правой полуплоскости;
, вершина расположена в правой полуплоскости;
Г. При  , вершина расположена в левой полуплоскости.
, вершина расположена в левой полуплоскости.
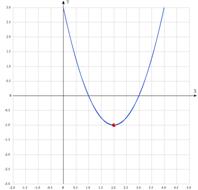
Пример: 
Решение: вычислим координаты вершины  . Построим параболу, ветви которой направлены вверх, т.к.
. Построим параболу, ветви которой направлены вверх, т.к. :
:
4) ![]() – функция квадратного корня.
– функция квадратного корня. 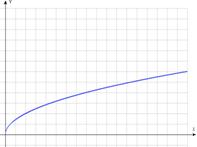
5)  – простейшая кубическая функция (график – кубическая парабола).
– простейшая кубическая функция (график – кубическая парабола).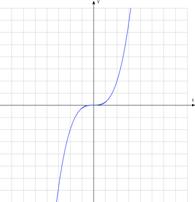
6)  – простейшая дробно-рациональная функция (график – гипербола).
– простейшая дробно-рациональная функция (график – гипербола).
В данном случае оси координат являются асимптотами графика функции  .
.
Асимптота – это прямая, к которой бесконечно близко приближается график функции, но никогда ее не достигает.
В простейшей гиперболе при стремлении аргумента к бесконечности график бесконечно прижимается к оси абсцисс, а при стремлении аргумента к нулю – к оси ординат, но гипербола никогда не пересекает осей.
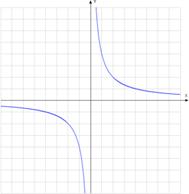
Кроме того, для графика функции  при
при  правая ветвь гиперболы расположена над осью абсцисс, а левая под осью; при
правая ветвь гиперболы расположена над осью абсцисс, а левая под осью; при  правая ветвь гиперболы расположена под осью абсцисс, а левая над осью.
правая ветвь гиперболы расположена под осью абсцисс, а левая над осью.
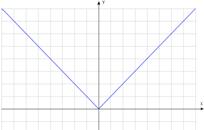
7)  – простейшая функция модуля.
– простейшая функция модуля.
Понятие функциональной зависимости
Область определения и область значений
Область определения функции – это множество значений аргумента, для которых функция имеет смысл. Иными словами, это допустимые значения икса. Это множество принято обозначать D или D(x).
Понятия четности и монотонности
Функция называется четной, если для всех значений аргумента верно следующее –при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так
4. Функция f(x) невозрастает, если на некотором интервале, если для любых двух точек
Обратные функции
Периодические функции
Функция
Понятие ГМТ
Функциональная зависимость устанавливает правило, согласно которому по значению независимой переменной – аргумента, можно найти значение зависимой переменной – функции. Слово функция употребляют в двух значениях: это и сама функциональная зависимость, и зависимая переменная.
Самое главное требование к функциональной зависимости: единственность от аргумента к функции. Это означает, что каждому значению аргумента может соответствовать единственное значение функции, в то время как одному значению функции может соответствовать сколь угодно много значений аргумента.
Функция - это закон соответствия между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует только одно определенное значение другой величины y (функции или зависимой переменной).
Основные способы задания числовых функций:
1. Аналитический способ – задание функции с помощью формулы.
Обозначать в общем виде такую формулу принято обычно как 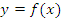 , где под x понимают аргумент, а под y значение функции.
, где под x понимают аргумент, а под y значение функции.
2. Табличный способ – задание функции с помощью таблицы связанных друг с другом значений.
3. Графический способ – задание функции с помощью изображения точек в системе координат, когда одной координате точек поставлена в однозначное соответствие другая ее координата.
Если функция задана аналитически, как это чаще всего бывает, то в таком случае удобнее всего сначала найти те значения аргумента, при которых функция не имеет смысла, и исключить их из множества действительных чисел.
Основные случаи, в которых необходимо искать не имеющие смысла для функции аргументы:
1. Наличие в функции деления на выражение, содержащее неизвестную. В таком случае исключаются те аргументы, при которых возникает деление на ноль.
2. Присутствие в функции корня четной степени из выражения, содержащего неизвестную. При этом необходимо исключить аргументы, при которых подкоренное выражение отрицательно, в таком случае удобно сразу накладывать условие, что подкоренное выражение больше или равно нулю.
3. Наличие в функции логарифмов, содержащих неизвестные выражения. В общем виде это можно записать так: если функция содержит 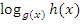 , где g(x) и h(x) - это выражения, содержащие неизвестную, то областью определения будет решение системы неравенств
, где g(x) и h(x) - это выражения, содержащие неизвестную, то областью определения будет решение системы неравенств 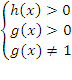 .
.
Область значений функции – это множество значений функции, которые она принимает в своей области определения. Т.е. в стандартной записи функции это значения ее игрека. Множество значений функции принято обозначать E или E(y).
Задания на поиск области значений функции в ВНО встречаются достаточно редко. .
.
График такой функции симметричен относительно оси 0y.
Пример: 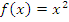 .
. 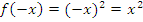 – функция четная.
– функция четная.
Функция называется нечетной, если для всех значений аргумента верно следующее – при изменении знака аргумента, она меняет свое значение на противоположное. Формульная запись этого выглядит так 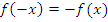 .
.
График такой функции симметричен относительно начала координат.
Пример: 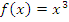 .
. 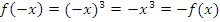 – функция нечетная.
– функция нечетная.
Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида. У таких функций нет симметрии относительно оси 0y и начала координат.
Важным свойством функции является ее монотонность. Выделяют следующие виды монотонности функций:
1. Функция f(x) возрастает, если на некотором интервале, если для любых двух точек 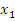 и
и 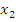 этого интервала таких, что
этого интервала таких, что 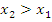 выполнено, что
выполнено, что 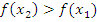 . Т.е. большему значению аргумента соответствует большее значение функции;
. Т.е. большему значению аргумента соответствует большее значение функции;
2. Функция f(x) убывает, если на некотором интервале, если для любых двух точек 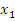 и
и 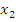 этого интервала таких, что
этого интервала таких, что 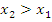 выполнено, что
выполнено, что 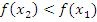 . Т.е. большему значению аргумента соответствует меньшее значение функции;
. Т.е. большему значению аргумента соответствует меньшее значение функции;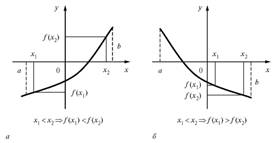
3. Функция f(x) неубывает, если на некотором интервале, если для любых двух точек 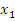 и
и 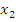 этого интервала таких, что
этого интервала таких, что 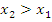 выполнено, что
выполнено, что 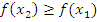 ;
;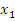 и
и 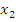 этого интервала таких, что
этого интервала таких, что 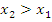 выполнено, что
выполнено, что 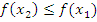 .
.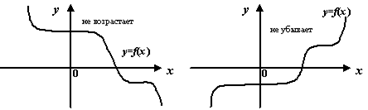
Для первых двух случаев еще применяют термин «строгая монотонность».
Два последних случая являются специфическими и задаются обычно в виде композиции из нескольких функций.
Пример: Функция 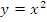 монотонно убывает при
монотонно убывает при 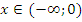 и монотонно возрастает при
и монотонно возрастает при 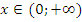 .
.
Если функция 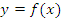 достигает каждого своего значения в единственной точке ее области определения, то можно задать функцию
достигает каждого своего значения в единственной точке ее области определения, то можно задать функцию 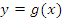 , которая называется обратной к функции
, которая называется обратной к функции 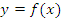 . Причем, для каждого a из области определения f, если
. Причем, для каждого a из области определения f, если 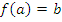 , то
, то 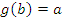 . Функции f и g называются взаимнообратными.
. Функции f и g называются взаимнообратными.
График обратной функции симметричен графику прямой функции относительно прямой 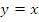 .
.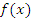 называется периодической с периодом
называется периодической с периодом 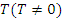 , если для любого x верно: если функция определена в одной из точек x или
, если для любого x верно: если функция определена в одной из точек x или 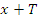 , то она определена и во второй точке, а значения функции в обеих точках равны, то есть
, то она определена и во второй точке, а значения функции в обеих точках равны, то есть 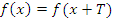 .
.
Число T называется периодом функции.
Все тригонометрические функции являются периодическими.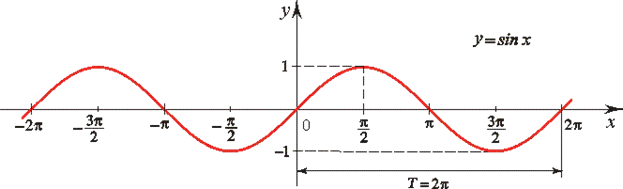
Графическое изображение однозначной функции называют построением графика функции, а изображение многозначной функции – построением геометрического места точек или ГМТ.
Пример: Графическое изображение уравнения 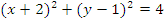 будет ГМТ, а конкретно изображением окружности:
будет ГМТ, а конкретно изображением окружности: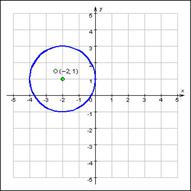
Тесты к уроку:
Онлайн-тест подготовки к ЗНО по математике №29 "Функции. Часть 1"
Полезные ссылки:












