Онлайн-урок №7 "Рациональные уравнения. Уравнения высших степеней"
Онлайн-урок "Уравнения высших степеней. Замена переменных. Биквадратные уравнения"
19.11.2015 в 18.30
Конспекты к уроку:
Понятие ОДЗ
Областью допустимых значений (ОДЗ) алгебраического выражения называют множество всех допустимых совокупностей значений букв, входящих в это выражение.
В частности знаменатель дроби не может быть равен нулю, поэтому значения переменных, при которых знаменатель равен нулю, недопустимы – не входят в ОДЗ
Пример: найти ОДЗ выражения  .
.
Решение: знаменатели обеих дробей не могут быть равны нулю, имеем систему:
![]()
Ответ: x≠±3.
Решение уравнений вида 
Произведение выражений равно нулю тогда и только тогда, когда одно из них равно нулю, а остальные при этом существуют. Поэтому уравнение вида  заменяется совокупностью уравнений:
заменяется совокупностью уравнений:
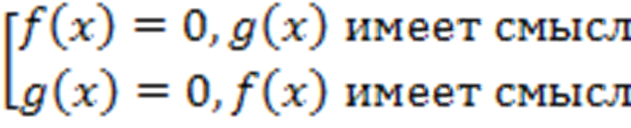
Пример: решить уравнение  .
.
Решение: ![]()
Ответ: -2,5;1.
Решение уравнений вида 
Дробь равна нулю тогда и только тогда, когда числитель ее равен нулю, а знаменатель при этом не равен нулю. Поэтому уравнения вида  заменяются совокупностью:
заменяются совокупностью: 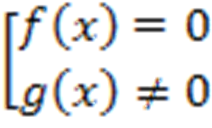
Пример: решить уравнение  .
.
Решение: 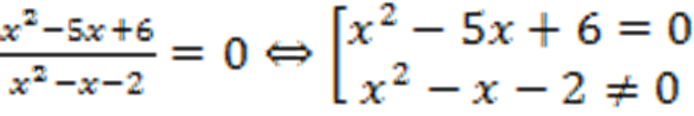
Корни квадратных уравнений определяем по теореме Виета: ![]() .
.
Ответ: 3.
Уравнения высших степеней. Метод замены переменных
Если в уравнении содержится переменная, степень которой выше 2, то такое уравнение называется уравнением высшей степени. Для решения уравнений высших степеней существует несколько наиболее распространенных методов:
1) Метод замены переменных;
2) Подбора корней;
3) Разложения на множители.
Метод замены переменных
Пример: решить уравнение 
Решение: очевидна замена переменных:  .
.
Получается уравнение:  . Согласно теореме Виета его корни:
. Согласно теореме Виета его корни:
В исходных переменных:![]()
Ответ: ±1; ±3.
Пример: решить уравнение  .
.
Решение: нужно сгруппировать крайние и средние скобки: ⇔
⇔ .
.
Можно заметить, что удобна замена:  , тогда получим уравнение
, тогда получим уравнение  ⇔
⇔ ⇔
⇔ . Согласно теореме Виета корни уравнения:
. Согласно теореме Виета корни уравнения:  .
.
В исходных переменных: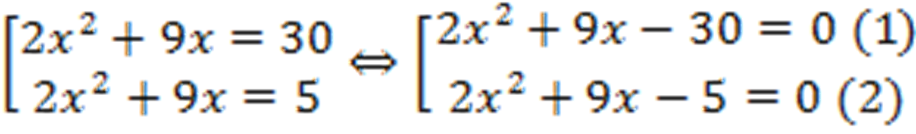
Дискриминанты уравнений: .
.
Корни первого уравнения: 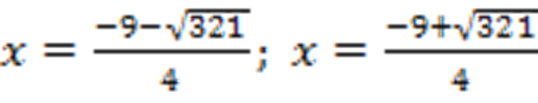 .
.
Корни второго уравнения:  .
.
Ответ: 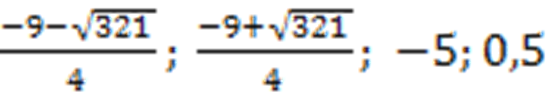 .
.
Замечание: метод подбора корней интуитивно понятен, а метод разложения на множители не требует примеров, т.к. разложение выражений на множители и решение уравнений вида  уже изучалось.
уже изучалось.
Биквадратные уравнения
Уравнение вида  называется биквадратным. Такие уравнения решаются приведением к квадратному уравнению с помощью замены вида
называется биквадратным. Такие уравнения решаются приведением к квадратному уравнению с помощью замены вида  .
.
Пример: решить уравнение .
.
Решение: согласно правилу выполним замену  , тогда:
, тогда:  .
.
В исходных переменных: 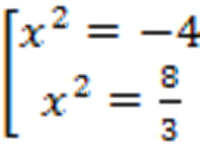 . Первое уравнение не имеет смысла, второе уравнение имеет два корня
. Первое уравнение не имеет смысла, второе уравнение имеет два корня 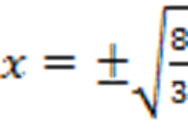 .
.
Ответ: ![]() .
.
Тесты к уроку:
Онлайн-тест подготовки к ЗНО по математике №9 "Рациональные уравнения. Уравнения высших степеней"
Полезные ссылки:












