Онлайн-урок №5 "Линейные уравнения и их системы"
Онлайн-урок "Линейные уравнения и их системы"
29.10.2015 в 18.30
Конспекты к уроку:
Равенства и их свойства, уравнение с одной переменной
Свойства равенств:
1) К обеим частям равенства можно прибавить или отнять любое численное выражение, имеющее смысл, при этом равенство не изменится:  ;
;
2) Обе части равенства можно умножить или разделить (кроме нуля) на любое численное выражение, имеющее смысл, при этом равенство не изменится:  ;
;
3) Обе части равенства можно возвести в одну и ту же нечетную степень, при этом равенство не изменится:  ;
;
4) Обе части равенства (если они обе положительны) можно возвести в одну и ту же четную степень, при этом равенство не изменится:  .
.
Равенство, содержащее одну переменную ( ), называется уравнением с одной переменной. Корнем уравнения называется такое значение переменной, при котором выражение обращается в верное числовое равенство. Решить уравнение означает найти все его корни или доказать, что корней нет.
), называется уравнением с одной переменной. Корнем уравнения называется такое значение переменной, при котором выражение обращается в верное числовое равенство. Решить уравнение означает найти все его корни или доказать, что корней нет.
Уравнения, имеющие одинаковые корни, называются равносильными.
Равносильные преобразования уравнений:
В уравнении можно перенести любое слагаемое из одной части в другую, сменив его знак на противоположный:  ⇔
⇔ ;
;
Обе части уравнения можно умножить или разделить на любое отличное от нуля число:  ⇔
⇔ .
.
Линейные уравнения
Уравнение вида  и все, которые к нему сводятся, называются линейными уравнениями с одной переменной. Здесь
и все, которые к нему сводятся, называются линейными уравнениями с одной переменной. Здесь  – произвольные действительные числа,
– произвольные действительные числа,  – переменная; коэффициент
– переменная; коэффициент  называют коэффициентом при переменной, коэффициент
называют коэффициентом при переменной, коэффициент  – свободным членом.
– свободным членом.
Линейное уравнение может содержать множество подобных слагаемых, в таком случае его сначала необходимо свести к простейшему виду, а затем решить.
При решении линейных уравнений есть три случая:
1) a≠0: в таком случае уравнение имеет единственный корень  ;
;
2) a=0,b=0: в этом случае уравнение превращается в равенство  , что верно при любом действительном
, что верно при любом действительном  , поэтому имеет бесчисленное множество решений;
, поэтому имеет бесчисленное множество решений;
3)a=0,b≠0: в этом случае имеем равенство  ≠
≠ , что неверно ни при каком значении
, что неверно ни при каком значении  и уравнение не имеет решений.
и уравнение не имеет решений.
Пример: решить уравнение  ⇔
⇔ ⇔
⇔ ⇔
⇔ .
.
Уравнения, которые сводятся к линейным
Пример: решить уравнение  .
.
Решение:  ⇔
⇔ ⇔
⇔ ⇔
⇔ ⇔
⇔ ⇔
⇔
Ответ: -23/17.
Пример: решить уравнение .
.
Решение:  ⇔
⇔ ⇔
⇔ ⇔
⇔
⇔ ⇔
⇔ .
.
Ответ: -12/7.
Неполные квадратные уравнения
Уравнение вида  называется квадратным. Здесь
называется квадратным. Здесь  – действительные числа,
– действительные числа,  – переменная.
– переменная.
Квадратное уравнение может быть неполным, если один из коэффициентов  равен нулю, или оба они равны нулю:
равен нулю, или оба они равны нулю:  ;
;  ;
;  .
.
Решение неполных квадратных уравнений:
Нужно разложить левую часть на множители:  . Произведение равно нулю только тогда, когда один из множителей равен нулю, а остальные при этом существуют:
. Произведение равно нулю только тогда, когда один из множителей равен нулю, а остальные при этом существуют: 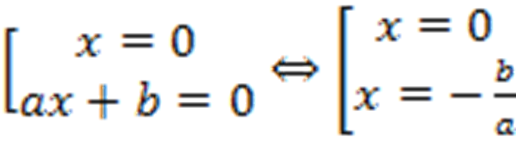
 .
.
Разделим уравнение на коэффициент при  . Согласно свойствам квадратичной функции, левая часть может принимать только неотрицательные значения, поэтому:
. Согласно свойствам квадратичной функции, левая часть может принимать только неотрицательные значения, поэтому: 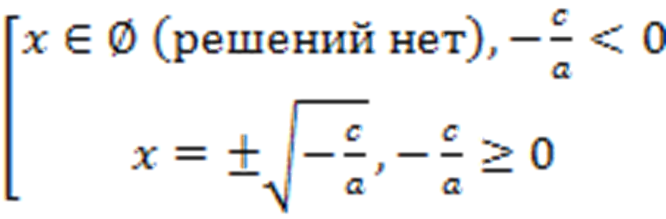
 .
.
Данное уравнение имеет единственное решение  . Обратим внимание, что коэффициент a мы считаем ненулевым.
. Обратим внимание, что коэффициент a мы считаем ненулевым.
Пример: решить уравнение  .
.
Решение:
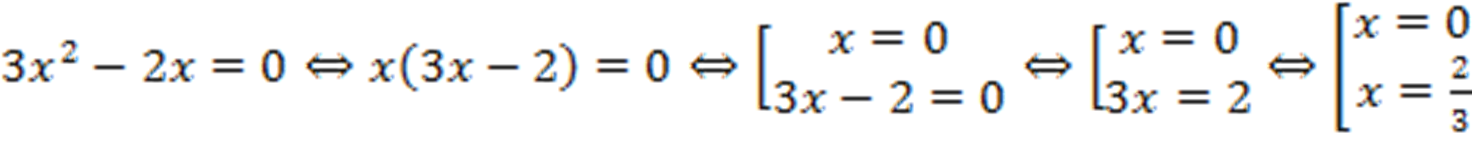
Ответ: 0; 2/3.
Дискриминант
Для поиска корней полного квадратного уравнения введено понятие дискриминанта. Это выражение вида:  , где
, где  – коэффициенты квадратного уравнения.
– коэффициенты квадратного уравнения.
В зависимости от значения дискриминанта можно выяснить наличие корней у квадратного уравнения:
1) D>0: уравнение имеет два различных корня, которые определяются по формуле 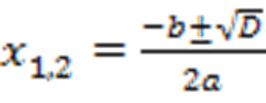 .
.
Отметим, что если коэффициент  кратен четырем, имеет место формула:
кратен четырем, имеет место формула:
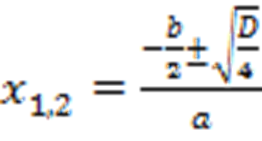 .
.
2) D=0: уравнение имеет два совпадающих корня, но принято говорить – уравнение имеет один корень  .
.
3) D<0: уравнение не имеет корней.
Пример: решить уравнение  .
.
Решение: Находим дискриминант:  . Дискриминант положителен – уравнение имеет два корня:
. Дискриминант положителен – уравнение имеет два корня:
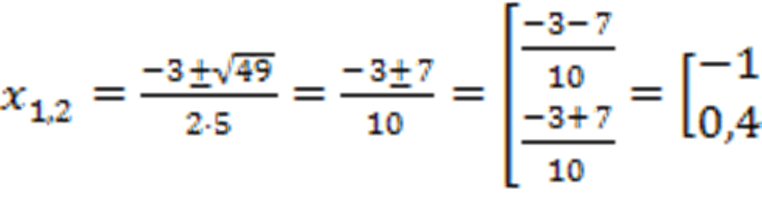
Ответ: -1;0,4.
Теорема Виета
Пусть задано произвольное квадратное уравнение: 
Прямая теорема Виета – сумма корней приведенного квадратного уравнения равна коэффициенту при  , взятому с противоположным знаком, а произведение корней равно свободному члену:
, взятому с противоположным знаком, а произведение корней равно свободному члену: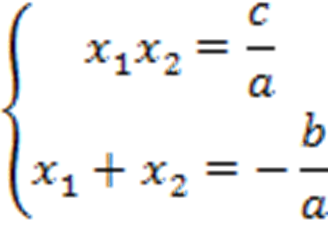
Обратная теорема Виета – если верно, что 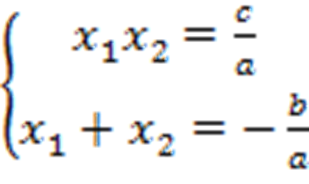 , то
, то  и
и  являются корнями квадратного уравнения:
являются корнями квадратного уравнения:  .
.
Замечание: все квадратные уравнения можно решать с использованием дискриминанта, другие способы применяются из соображений ускорения процесса решения.
Пример: найти корни уравнения, не решая его:  .
.
Решение: согласно прямой теореме Виета: 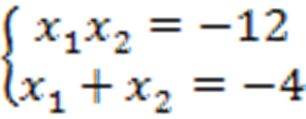 . Методом подбора определяем:
. Методом подбора определяем:  .
.
Ответ: 2;-6.
Разложение квадратного трехчлена на множители
Если квадратное уравнение  имеет корни
имеет корни  и
и  , то квадратный трехчлен
, то квадратный трехчлен  раскладывается на множители следующим образом:
раскладывается на множители следующим образом:
Пример: разложить на множители  .
.
Решение: рассмотрим квадратное уравнение:  . Согласно теореме Виета его корни:
. Согласно теореме Виета его корни:  . Тогда имеем разложение:
. Тогда имеем разложение:  .
.
Ответ:  .
.
Решение уравнений, содержащих неизвестную под модулем Уравнения, в которых переменная стоит под знаком модуля и такой модуль один, в простейшем случае сводятся к уравнениям вида Объединив решение с ограничением на правую часть уравнения, получаем При Системы линейных уравнений Система вида Заключается в том, что в одном из уравнений системы нужно выразить одну переменную через другую и подставить полученное выражение во второе уравнение системы. Заключается в том, что нужно получить противоположные коэффициенты при одной из переменных уравнения и сложить уравнения, при этом избавившись от одной переменной. Таким образом, решение системы сводится к решению линейного уравнения с одной переменной. Получаем Заключается в построении графиков двух линейных функций. Если прямые пересеклись – координаты точки пересечения будут единственным решением системы. Если прямые параллельны или совпали, то система не имеет решений или, соответственно, имеет бесконечно много решений. Количество решений системы линейных уравнений
Система двух линейных уравнений с графической точки зрения представляет собой две прямые, построенные в системе координат. Две прямые могут пересекаться только в одной точке. Также они могут совпадать или быть параллельными. Очевидно, что система двух линейных уравнений имеет только три варианта решения:  , где a – действительное число. Если
, где a – действительное число. Если  , то решений нет, если
, то решений нет, если  , то решение подобного уравнения:
, то решение подобного уравнения: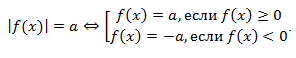
Пример:  .
.
Решение: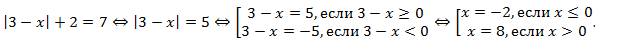
Ответ: -2;8.
Также уравнение с одним модулем может иметь вид  . Решение такого уравнения аналогично.
. Решение такого уравнения аналогично.
Пример: 
Решение: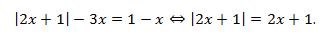
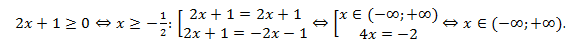
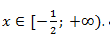
Ответ: 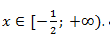 .
.
При решении уравнений с несколькими модулями вида нужно придерживаться алгоритма:
нужно придерживаться алгоритма:
Определить нули подмодульных выражений, решив уравнения:  и т.д.;
и т.д.;
Разбить множество значений аргумента на интервалы определенными в п.1 нулями;
Определить знаки подмодульных выражений на каждом интервале;
Рассмотреть решение уравнения на каждом интервале отдельно, раскрыв модули с учетом знаков подмодульных выражений.
Пример:  .
.
Решение: 1. Определяем нули: 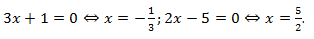
2. Множество значений аргумента разбито на интервалы:  .
.
3. Определяем знаки подмодульных выражений:
4. Рассмотрим решение уравнения для трех случаев. :
: 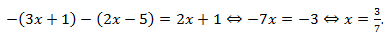 . Найденный корень не входит в рассматриваемый интервал.
. Найденный корень не входит в рассматриваемый интервал.
При  :
: 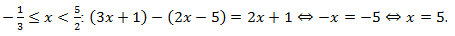 Найденный корень не входит в рассматриваемый интервал.
Найденный корень не входит в рассматриваемый интервал.
При  :
: 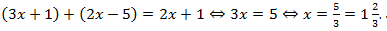 . Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.
. Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.
Ответ: корней нет.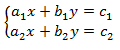 называется системой линейных уравнений с двумя переменными, здесь
называется системой линейных уравнений с двумя переменными, здесь  – действительные числа. Решить систему означает найти все пары значений
– действительные числа. Решить систему означает найти все пары значений  , которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.
, которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.
1. Метод подстановки.
Пример: 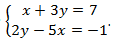
Решение: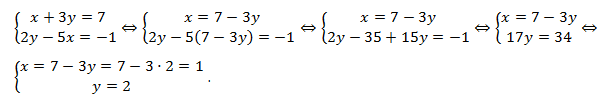
Ответ: (1;2).
2. Метод алгебраического сложения.
Пример: 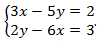
Решение: 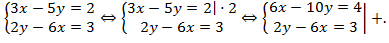
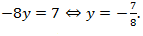
Ответ:  .
.
3. Графический метод.
Единственное решение (прямые пересекаются);
Нет решений (прямые параллельны);
Бесконечно много решений (прямые совпали).
Для системы 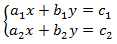 существует простой способ определить наличие решений:
существует простой способ определить наличие решений:
– если  , то система имеет бесконечное количество решений;
, то система имеет бесконечное количество решений;
– если  , то система не имеет решений;
, то система не имеет решений;
– если  , то система имеет одно решение.
, то система имеет одно решение.
Системы уравнений высших степеней
Системы, в которых одно из уравнений линейное, как правило, решаются методом подстановки. Если в системе оба уравнения нелинейные, то применяют также комбинирование уравнений с целью получения нового уравнения, которое можно разложить на простые множители.
Пример: 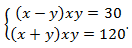
Решение: Нужно раскрыть скобки: 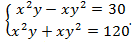 Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания:
Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания: 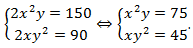 Нужно умножить уравнения системы:
Нужно умножить уравнения системы: 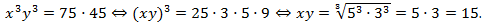 Теперь можно применить способ подстановки:
Теперь можно применить способ подстановки: 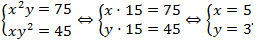
Ответ: 5;3.
Тесты к уроку:
Онлайн-тест подготовки к ЗНО по математике №8 "Линейные уравнения. Квадратные уравнения"
Полезные ссылки:
Решение уравнений, содержащих неизвестную под модулем Уравнения, в которых переменная стоит под знаком модуля и такой модуль один, в простейшем случае сводятся к уравнениям вида  , где a – действительное число. Если
, где a – действительное число. Если  , то решений нет, если
, то решений нет, если  , то решение подобного уравнения:consp-mat-11-1Пример:
, то решение подобного уравнения:consp-mat-11-1Пример:  .Решение:consp-mat-11-2Ответ: -2;8.Также уравнение с одним модулем может иметь вид
.Решение:consp-mat-11-2Ответ: -2;8.Также уравнение с одним модулем может иметь вид  . Решение такого уравнения аналогично.Пример:
. Решение такого уравнения аналогично.Пример:  Решение:consp-mat-11-3 consp-mat-11-4Объединив решение с ограничением на правую часть уравнения, получаем consp-mat-11-5Ответ: consp-mat-11-5.При решении уравнений с несколькими модулями вида
Решение:consp-mat-11-3 consp-mat-11-4Объединив решение с ограничением на правую часть уравнения, получаем consp-mat-11-5Ответ: consp-mat-11-5.При решении уравнений с несколькими модулями вида нужно придерживаться алгоритма:Определить нули подмодульных выражений, решив уравнения:
нужно придерживаться алгоритма:Определить нули подмодульных выражений, решив уравнения:  и т.д.;Разбить множество значений аргумента на интервалы определенными в п.1 нулями;Определить знаки подмодульных выражений на каждом интервале;Рассмотреть решение уравнения на каждом интервале отдельно, раскрыв модули с учетом знаков подмодульных выражений.Пример:
и т.д.;Разбить множество значений аргумента на интервалы определенными в п.1 нулями;Определить знаки подмодульных выражений на каждом интервале;Рассмотреть решение уравнения на каждом интервале отдельно, раскрыв модули с учетом знаков подмодульных выражений.Пример:  . Решение: 1. Определяем нули: consp-mat-11-6 2. Множество значений аргумента разбито на интервалы:
. Решение: 1. Определяем нули: consp-mat-11-6 2. Множество значений аргумента разбито на интервалы:  . 3. Определяем знаки подмодульных выражений:consp-mat-11-84. Рассмотрим решение уравнения для трех случаев.При
. 3. Определяем знаки подмодульных выражений:consp-mat-11-84. Рассмотрим решение уравнения для трех случаев.При  : consp-mat-11-9. Найденный корень не входит в рассматриваемый интервал. При
: consp-mat-11-9. Найденный корень не входит в рассматриваемый интервал. При  : consp-mat-11-10 Найденный корень не входит в рассматриваемый интервал. При
: consp-mat-11-10 Найденный корень не входит в рассматриваемый интервал. При  : consp-mat-11-11. Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.Ответ: корней нет. Системы линейных уравнений Система вида consp-mat-11-12 называется системой линейных уравнений с двумя переменными, здесь
: consp-mat-11-11. Найденный корень не входит в рассматриваемый интервал. Таким образом, рассматриваемое уравнение не имеет корней.Ответ: корней нет. Системы линейных уравнений Система вида consp-mat-11-12 называется системой линейных уравнений с двумя переменными, здесь  – действительные числа. Решить систему означает найти все пары значений
– действительные числа. Решить систему означает найти все пары значений  , которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.1. Метод подстановки.Заключается в том, что в одном из уравнений системы нужно выразить одну переменную через другую и подставить полученное выражение во второе уравнение системы.Пример: consp-mat-11-13Решение:consp-mat-11-14Ответ: (1;2).2. Метод алгебраического сложения.Заключается в том, что нужно получить противоположные коэффициенты при одной из переменных уравнения и сложить уравнения, при этом избавившись от одной переменной. Таким образом, решение системы сводится к решению линейного уравнения с одной переменной.Пример: consp-mat-11-15Решение: consp-mat-11-16Получаем consp-mat-11-17Ответ:
, которые обращают в верные численные равенства сразу оба уравнения системы, или доказать, что их нет. Существует несколько методов решения систем линейных уравнений.1. Метод подстановки.Заключается в том, что в одном из уравнений системы нужно выразить одну переменную через другую и подставить полученное выражение во второе уравнение системы.Пример: consp-mat-11-13Решение:consp-mat-11-14Ответ: (1;2).2. Метод алгебраического сложения.Заключается в том, что нужно получить противоположные коэффициенты при одной из переменных уравнения и сложить уравнения, при этом избавившись от одной переменной. Таким образом, решение системы сводится к решению линейного уравнения с одной переменной.Пример: consp-mat-11-15Решение: consp-mat-11-16Получаем consp-mat-11-17Ответ:  .3. Графический метод.Заключается в построении графиков двух линейных функций. Если прямые пересеклись – координаты точки пересечения будут единственным решением системы. Если прямые параллельны или совпали, то система не имеет решений или, соответственно, имеет бесконечно много решений. Количество решений системы линейных уравнений Система двух линейных уравнений с графической точки зрения представляет собой две прямые, построенные в системе координат. Две прямые могут пересекаться только в одной точке. Также они могут совпадать или быть параллельными. Очевидно, что система двух линейных уравнений имеет только три варианта решения:Единственное решение (прямые пересекаются);Нет решений (прямые параллельны);Бесконечно много решений (прямые совпали).Для системы consp-mat-11-19 существует простой способ определить наличие решений:– если
.3. Графический метод.Заключается в построении графиков двух линейных функций. Если прямые пересеклись – координаты точки пересечения будут единственным решением системы. Если прямые параллельны или совпали, то система не имеет решений или, соответственно, имеет бесконечно много решений. Количество решений системы линейных уравнений Система двух линейных уравнений с графической точки зрения представляет собой две прямые, построенные в системе координат. Две прямые могут пересекаться только в одной точке. Также они могут совпадать или быть параллельными. Очевидно, что система двух линейных уравнений имеет только три варианта решения:Единственное решение (прямые пересекаются);Нет решений (прямые параллельны);Бесконечно много решений (прямые совпали).Для системы consp-mat-11-19 существует простой способ определить наличие решений:– если  , то система имеет бесконечное количество решений;– если
, то система имеет бесконечное количество решений;– если  , то система не имеет решений;– если
, то система не имеет решений;– если  , то система имеет одно решение.Системы уравнений высших степенейСистемы, в которых одно из уравнений линейное, как правило, решаются методом подстановки. Если в системе оба уравнения нелинейные, то применяют также комбинирование уравнений с целью получения нового уравнения, которое можно разложить на простые множители.Пример: consp-mat-11-20Решение: Нужно раскрыть скобки: consp-mat-11-21 Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания: consp-mat-11-22 Нужно умножить уравнения системы: consp-mat-11-23 Теперь можно применить способ подстановки: consp-mat-11-24Ответ: 5;3.
, то система имеет одно решение.Системы уравнений высших степенейСистемы, в которых одно из уравнений линейное, как правило, решаются методом подстановки. Если в системе оба уравнения нелинейные, то применяют также комбинирование уравнений с целью получения нового уравнения, которое можно разложить на простые множители.Пример: consp-mat-11-20Решение: Нужно раскрыть скобки: consp-mat-11-21 Теперь нужно составить новую систему. Первое уравнение получается путем сложения уравнений системы, второе – путем вычитания: consp-mat-11-22 Нужно умножить уравнения системы: consp-mat-11-23 Теперь можно применить способ подстановки: consp-mat-11-24Ответ: 5;3.












