Онлайн-урок №4 "Корень n-ной степени из действительного числа. Обобщение понятия степени."

Понятие и свойства корня n-ной степени из действительного числа

Корнем -ой степени из действительного числа a(  ) называется такое число , что: , где .
Для чётных значений ≥0. 
Для нечётных значений  такого ограничения нет.
Для четных  используют понятие арифметического корня из числа , это неотрицательное число, -ная степень которого равна . 
Пример: арифметический квадратный корень из 16 равен 4, квадратный корень из 16 это ±4.
Свойства корня:

1)  (a,b≥0 при чётном n).
2)  (a≥0 при чётном n или k).
3) 
4) 
5) 

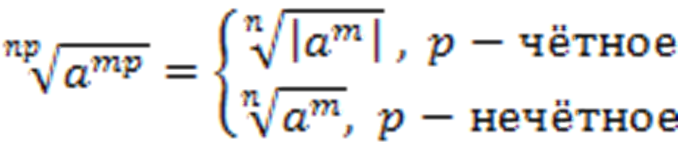
Вынесение и внесение множителя под знак корня

Чтобы вынести множитель из-под знака корня, необходимо подкоренное выражение представить в виде степени или произведения степеней с показателем, кратным показателю корня. 
Пример:

1)  ;  ; 
Чтобы внести множитель под знак корня, нужно возвести его в степень корня и после этого внести. 
Пример:

1)  ;  ;  (вносить минус под корень четной степени нельзя).

Избавление от иррациональности в знаменателе

Чтобы избавиться от иррациональности в знаменателе дроби, нужно всю дробь домножить на выражение, сопряженное к знаменателю. Основные ситуации, которые могут встретиться: 

1) Если в знаменателе стоит корень, который не входит в слагаемые, то числитель и знаменатель дроби нужно домножить на другой корень так, чтобы в результате этот корень можно было извлечь до целого выражения. 
Пример: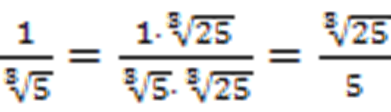 
2) Если в знаменателе стоит сумма или разность двух выражений и хотя бы одно из них содержит квадратный корень, нужно домножить на сопряжённое выражение – такое же выражение, но с противоположным знаком.
Пример: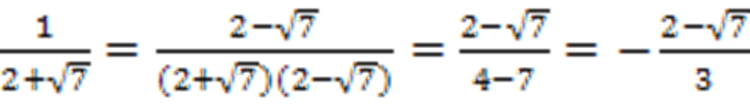 

Принцип «исчезновения» иррациональности основан на применении формулы разности квадратов.
3) Если в знаменателе стоит сумма или разность двух выражений и хотя бы одно из них содержит кубический корень, нужно домножить на неполный квадрат разности или суммы этих выражений – чтобы знаменатель свернуть по формуле суммы или разности кубов соответственно.
Пример: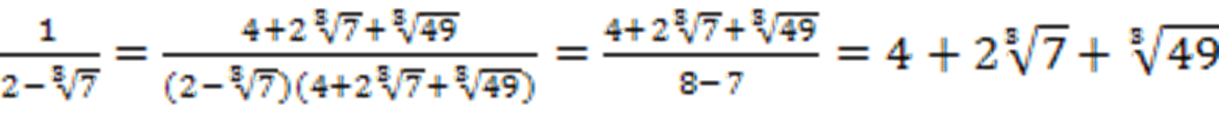 

Иррациональные выражения

Алгебраическое выражение называется иррациональным, если в нём присутствует операция извлечения корня из переменной. 
Пример: упростить выражение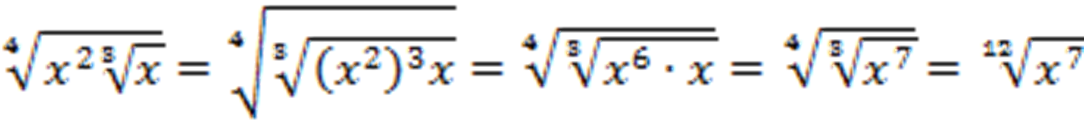 

Степень действительного числа с рациональным показателем

Ранее была рассмотрена степень с натуральным показателем и степень с отрицательным показателем. Степень с дробным (рациональным) показателем соответствует корню: 

Для степени с дробным показателем справедливы все свойства степени с натуральным и отрицательным показателем. Так, теперь степень с неотрицательным основанием a определена для любого рационального показателя.
Пример: 
Пример: упростить выражение

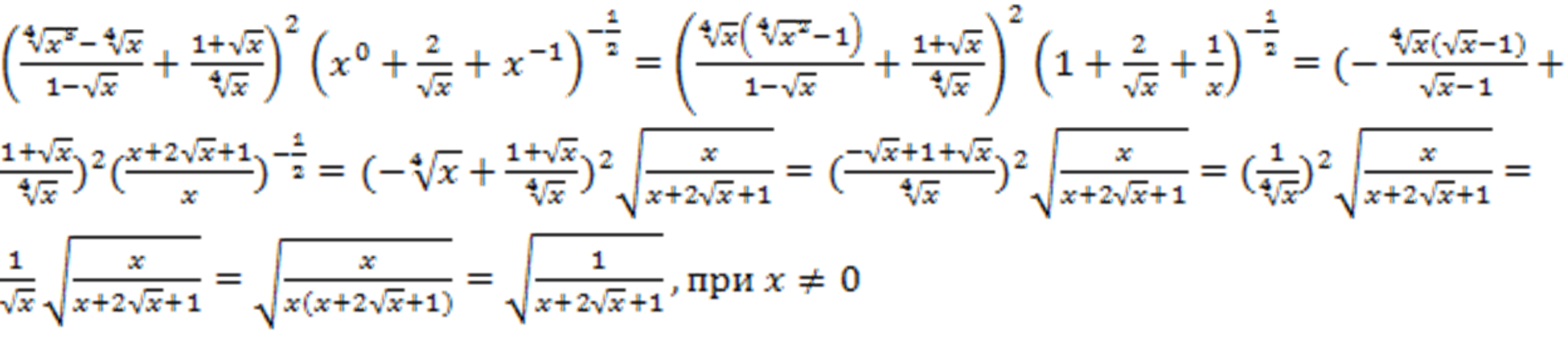
Пример 1: вычислить

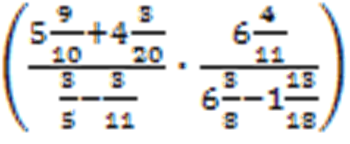
Решение: сначала нужно определить порядок действий:

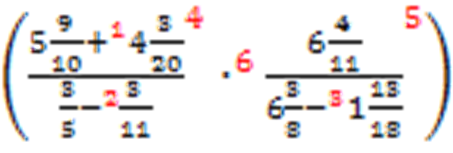
1. Сложение дробей:

2-3. Вычитание дробей:

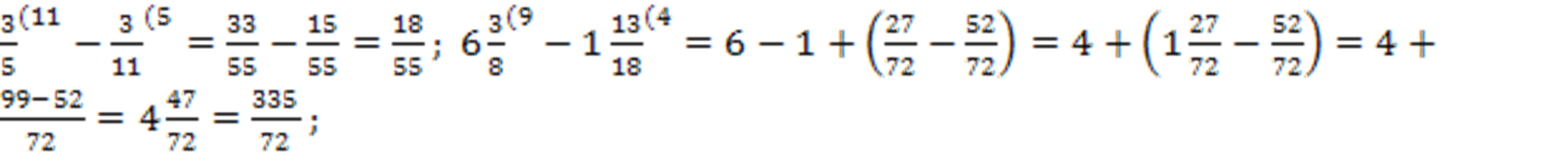
4-5. Деление дробей:

6. Умножение дробей:

Ответ: 42.

Пример 2: упростить выражение

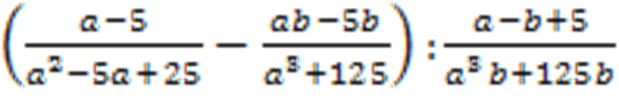
Решение: сначала нужно выполнить вычитание в скобках, для этого привести дроби к общему знаменателю с помощью ФСУ.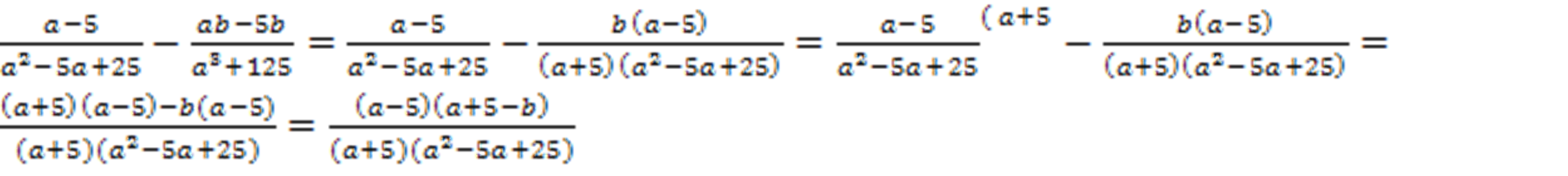 

Теперь нужно разделить дроби: 

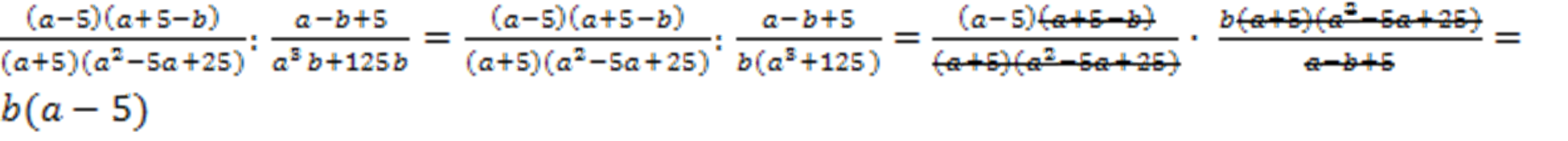
Ответ: .

Пример 3: вычислить

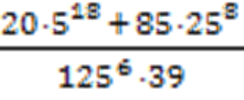
Решение: нужно во всех слагаемых выделить пятерку в максимальной степени, для этого разложить на простые множители: 

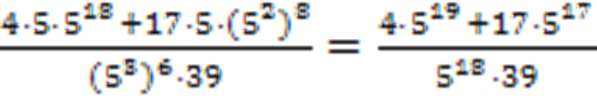
Теперь можно вынести в числителе общий множитель и сократить дробь:

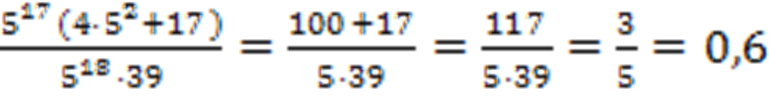
Ответ: 0,6.

Пример 4: вычислить значение выражения

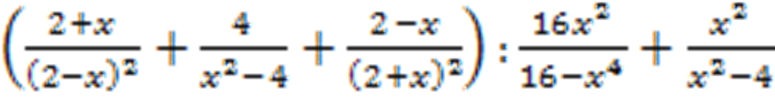 при x=12. 
Решение: сначала нужно выполнить сложение в скобках, для этого привести дроби к общему знаменателю с помощью ФСУ.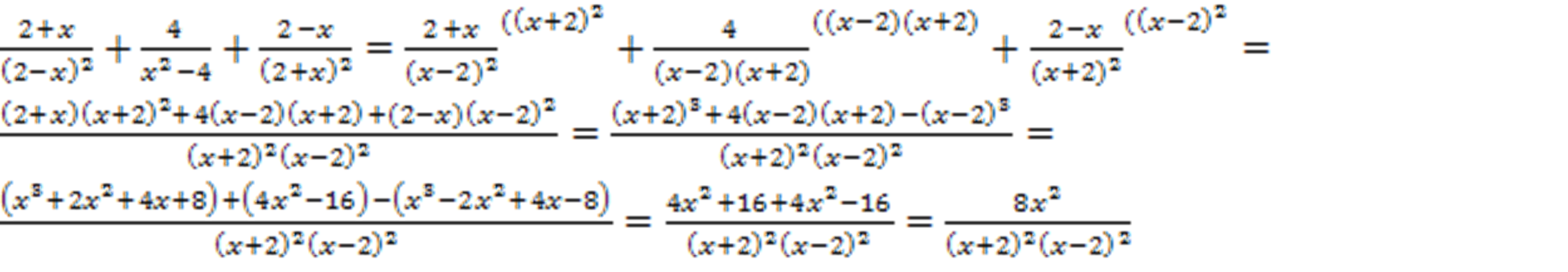

Теперь нужно разделить дроби:

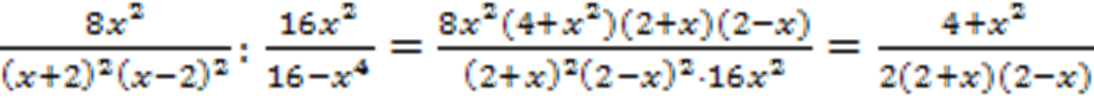
Осталось сложить дроби:

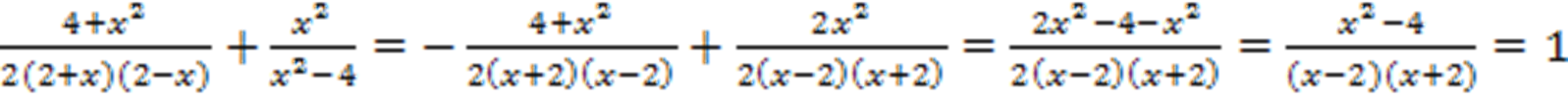
Как видим получилось численное значение, и подставлять значение переменной нет необходимости.
Ответ: 1.

Пример 5: вычислить

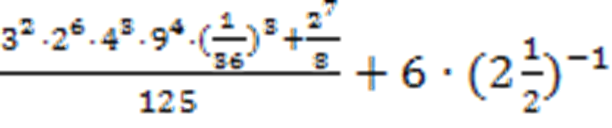
Решение:

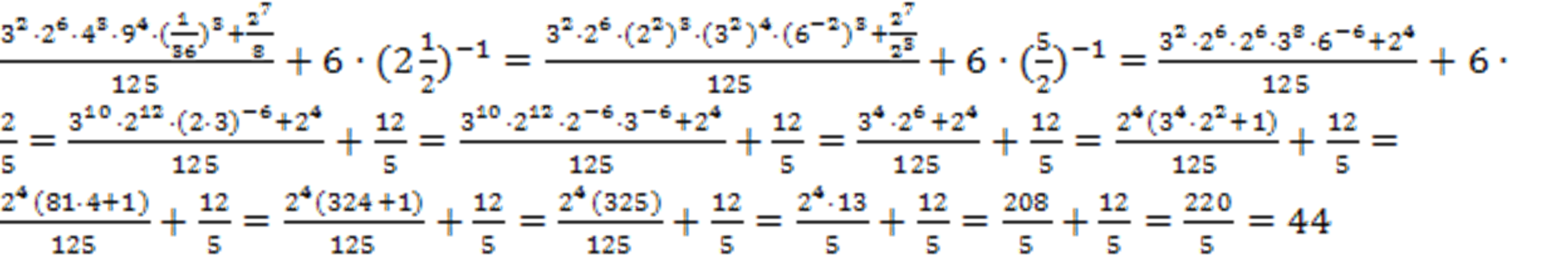
Ответ: 44.