Онлайн-урок №2 "Степень числа. Модуль"

Свойства степени с натуральным показателем

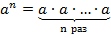 – степень с натуральным показателем, здесь a – основание степени, n – показатель степени;

Свойства степеней с одинаковыми основаниями:
1) 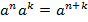 – для того, чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить тем же самым;
2) 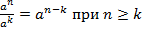 – чтобы разделить степени с одинаковым основанием, их показатели нужно вычесть, а основание оставить тем же самым; 
3) 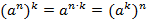 – для того, чтобы степень возвести в степень, нужно перемножить показатели степени, а основание оставить без изменений.

Некоторые важные равенства: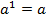

;
.

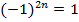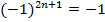Свойства степеней с одинаковыми показателями: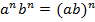
 – при умножении степеней с одинаковым показателем, нужно перемножить основания и возвести результат в исходную степень;
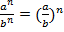, b≠0 – чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень.

Степень с нулевым показателем

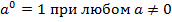 , т.к. .
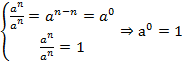Действие  не имеет смысла.

Степень с отрицательным показателем

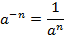
В случае, если дробь возводится в отрицательную степень, её можно упростить так:

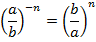
Упрощение выражений, содержащих степени

Пример: вычислить .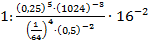

Решение: приведем все степени к основанию 2 и воспользуемся свойствами степеней с одинаковым основанием:.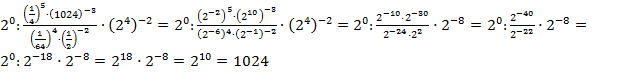

Ответ: 1024.

Одночлен и многочлен (общие сведения)

Одночлен – это математическое выражение, которое состоит из произведения чисел и переменных, каждая из которых может входить в произведение в некоторой степени. Пример: .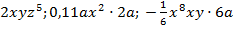

Стандартный вид одночлена – это произведение, составленное из числового множителя и степеней различных переменных, при чем каждая переменная входит в запись только один раз. Числовой множитель называется коэффициентом одночлена.

Для того, чтобы привести одночлен к стандартному виду, достаточно перемножить все числовые множители и поставить получившееся число на первое место. Затем перемножить все степени с одинаковым основанием.

Подобные одночлены – это одночлены с одинаковой буквенной частью. Подобные одночлены (слагаемые) можно складывать и вычитать – при этом действие производится только над коэффициентами, буквенная часть остается неизменной. Пример: 

2ax+7ax-3ax=(2+7-3)ax=6ax

Многочлен – это алгебраическое выражение, представляющее собой сумму/разность одночленов. Стандартным видом многочлена называется такая запись многочлена, при которой все входящие в него одночлены записаны в стандартном виде и приведены подобные слагаемые. Пример: 2x²-3x+5.

Сумма и разность многочленов, правила раскрытия скобок, приведение подобных слагаемых

При сложении или вычитании многочленов получается новый многочлен, вся суть операции заключается в том, чтобы привести этот новый многочлен к стандартному виду.
Приведение подобных слагаемых многочлена состоит в том, что нужно сложить или вычесть все входящие в него подобные одночлены между собой.
При раскрытии скобок в случае сложения и вычитания многочленов нужно знать, если перед скобкой стоит знак плюс, то скобки просто убираются и многочлен, который был в скобках, переписывается с сохранением всех знаков. Если же перед скобкой стоит знак минус, то когда скобки убираются, знак КАЖДОГО члена многочлена, стоявшего в этих скобках, меняется на противоположный. Здесь также поможет простое правило: «Плюс на плюс дает плюс, минус на плюс дает минус, минус на минус дает плюс». 
Пример: (2ab+x-xy)+(ab-5xy)-(6x-ab)=2ab+x-xy+ab-5xy-6x+ab=4ab-5x-6xy.

Умножение многочлена на многочлен

При умножении многочленов нужно соблюдать единственное, но очень важное правило: каждый член первого многочлена нужно умножить на каждый член второго многочлена и записать алгебраическую сумму полученных произведений. 
Пример: (2x+y)(x-a+1)=2x•x+2x•(-a)+2x•1+y•x+y•(-a)+y•1=2x²-2ax+2x+xy-ay+y. После выполнения умножения нужно привести многочлен к стандартному виду (в рассмотренном примере получен многочлен стандартного вида, поэтому приведение не нужно).

Модуль

Расстояние от точки на координатной прямой до нуля называется модулем числа, т.е. модулем координаты данной точки: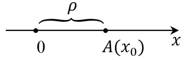
  

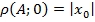
Следовательно, значение модуля всегда неотрицательно.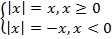
 – варианты раскрывания модуля.
Пример: 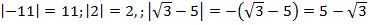 величина отрицательная).