Онлайн-урок №22 "Механические колебания."

Конспект 29. Механические колебания.

Раздел: КОЛЕБАНИЯ И ВОЛНЫ

Тема: Механические колебания и волны

1. Гармонические колебания

Определение. Колебания – это повторяющийся во времени процесс изменения состояний системы относительно какого-то состояния (положения) равновесия.
Определение. Механические колебания – движение, при котором тело (точка) проходит одни и те же координаты в пространстве через одинаковые промежутки времени.
Основные параметры колебательного движения: период, частота, циклическая частота, амплитуда.
Замечание. Как правило, когда говорят описать колебания, необходимо указать его основные параметры.
Определение. Период колебаний (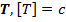) – это минимальное время между двумя одинаковыми состояниями колебательной системы (положениями точки в пространстве при механических колебаниях).
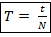 – период, с
Где N – число оборотов за время t
Определение. Частота колебаний (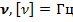) – количество колебаний в единицу времени.
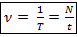– частота, Гц
Определение. Циклическая частота колебаний (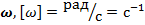) – мера частоты колебаний, показывающая количество колебаний за 2π секунд.
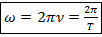 – циклическая частота,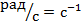 
Определение. Амплитуда колебаний – максимальное изменение величины, которая совершает периодические изменения, от ее среднего значения (положения равновесия).
Замечание. В зависимости от того, амплитуда колебаний какой величины рассматривается, используются различные обозначения. Например, амплитуда колебаний координаты тела 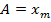, , 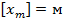амплитуда колебаний скорости тела 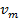, , 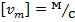амплитуда колебаний ускорения тела 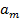,  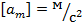и т.п.

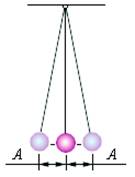
Замечание. За одно полное колебание тело проходит путь равный четырем амплитудам.
Определение. Гармонические колебания – колебания, при которых величина периодически изменяется по гармоническому закону, т.е. закону косинуса или синуса.
Координата точки (тела) при гармонических механических колебаниях: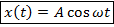
 – функция колебаний координаты, если они начинаются с точки максимального отклонения
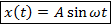– функция колебаний координаты, если они начинаются с положения равновесия
Замечание. A,ω – параметры колебательной системы (числа); x,t – переменные.
Построение графиков и описание функций гармонических механических колебаний:
1) 

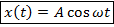
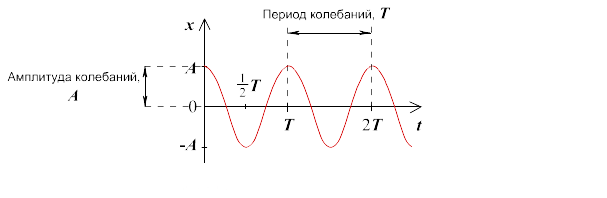
2) 

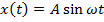
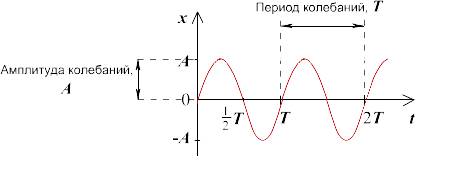
Определение. Фаза гармонических колебаний (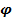,[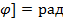) – аргумент функции косинуса или синуса, который определяет состояние колебательной системы в определенный момент времени. В общем случа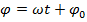е , где 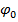 – начальная фаза колебаний.
Координата точки (тела) при гармонических механических колебаниях с начальной фазой: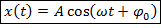


Замечание. Скорость – это первая производная координаты (механический смысл производной) 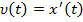, а ускорение – первая производная скорости или вторая производная координаты .
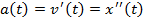Скорость точки (тела) при гармонических механических колебаниях с начальной фазой: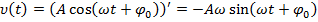


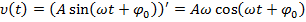
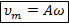 – амплитуда скорости, м/с
Замечание. 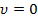 в крайней точке,  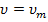в положении равновесия.
Ускорение точки (тела) при гармонических механических колебаниях с начальной фазой: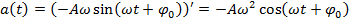


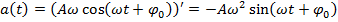
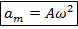 – амплитуда ускорения, м/с² 
Замечание. 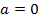 в положении равновесия,  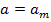в крайней точке.